子圖
設G=(VE)是一個圖若V是V的子集E是E的子集且E中的邊所關聯的頂點均在V中則G=(VE)也是一個圖並稱其
為G的子圖(Subgraph)
【例】圖給出了有向圖G l 的若干子圖;圖給出了無向圖G 的若干個子圖
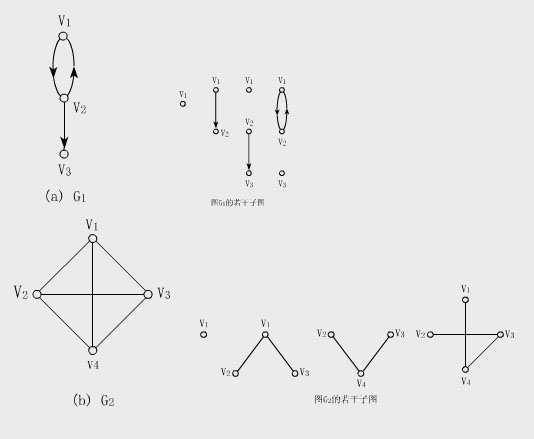
注意
設V={v v v }E={(v l v )(v v )}顯然V屬於V(G )E屬於E(G )但因為E中序偶對
(v v )所關聯的頂點v 不在V中所以(VE)不是圖也就不可能是G 的子圖
路徑(Path)
無向圖的路徑
在無向圖G中若存在一個頂點序列v p v i v i …v im v q 使得(v p v i )(v i v i )…(v
im v q )均屬於E(G)則稱頂點v p 到v q 存在一條路徑(Path)
有向圖的路徑
在有向圖G中路徑也是有向的它由E(G)中的有向邊…組成
路徑長度
路徑長度定義為該路徑上邊的數目
簡單路徑
若一條路徑上除了v p 和v q 可以相同外其余頂點均不相同則稱此路徑為一條簡單路徑
【例】在圖G 中頂點序列v l v v v 是一條從頂點v 到頂點v 的長度為的簡單路徑
【例】在圖G 中頂點序列v v v v v 是一條從頂點v 到頂點v 的長度為的路徑但不是簡單路徑;
簡單回路或簡單環(Cycle)
起點和終點相同(v p =v q )的簡單路徑稱為簡單回路或簡單環(Cycle)
【例】圖G 中頂點序列v v v v 是一個長度為的簡單環
【例】有向圖G 中頂點序列v v v 是一長度為的有向簡單環
有根圖和圖的根
在一個有向圖中若存在一個頂點v從該頂點有路徑可以到達圖中其它所有頂點則稱此有向圖為有根圖v稱作圖的根
From:http://tw.wingwit.com/Article/program/sjjg/201311/23856.html

