圖 - 圖的概念（四）

　　連通圖和連通分量

　　頂點間的連通性

　　在無向圖G中若從頂點v i 到頂點v j 有路徑(當然從v j 到v i 也一定有路徑)則稱v i 和v j 是連通的

　　連通圖

　　若V(G)中任意兩個不同的頂點v i 和v j 都連通(即有路徑)則稱G為連通圖(Connected Graph)

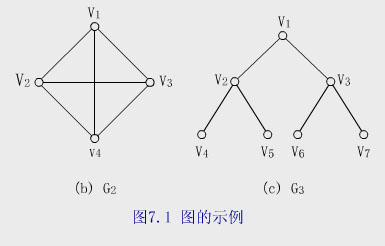
　　【例】圖G 和G 是連通圖

　　

　　連通分量

　　無向圖G的極大連通子圖稱為G的連通分量(Connected Component)

　　注意

　　① 任何連通圖的連通分量只有一個即是其自身

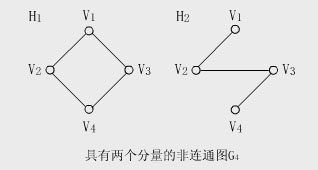
　　② 非連通的無向圖有多個連通分量

　　【例】下圖中的G 是非連通圖它有兩個連通分量H 和H

　　

　　強連通圖和強連通分量

　　強連通圖

　　有向圖G中若對於V(G)中任意兩個不同的頂點v i 和v j 都存在從v i 到v j 以及從v j 到v i 的路徑則稱G是強連通圖

　　強連通分量

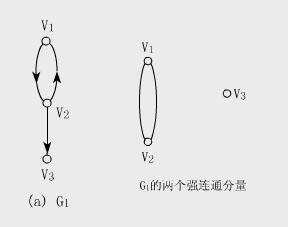
　　有向圖的極大強連通子圖稱為G的強連通分量

　　注意

　　① 強連通圖只有一個強連通分量即是其自身

　　② 非強連通的有向圖有多個強連分量

　　【例】下圖中的G 不是強連通圖因為v 到v 沒有路徑但它有兩個強連通分量如右圖所示

　　

　　網絡(Network)

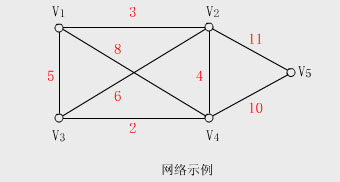
　　若將圖的每條邊都賦上一個權則稱這種帶權圖為網絡(Network)

　　注意

　　權是表示兩個頂點之間的距離耗費等具有某種意義的數

　　【例】下圖就是一個網絡的例子

　　

From:http://tw.wingwit.com/Article/program/sjjg/201311/23854.html