本章簡介
圖(Graph)是一種復雜的非線性結構在人工智能工程數學物理化學生物和計算機科學等領域中圖結構有著廣泛的
應用
本章先介紹圖的概念再介紹圖的存儲方法及有關圖的算法
圖的二元組定義
圖G由兩個集合V和E組成記為
G=(VE)
其中
V是頂點的有窮非空集合
E是V中頂點偶對(稱為邊)的有窮集
通常也將圖G的頂點集和邊集分別記為V(G)和E(G)E(G)可以是空集若E(G)為空則圖G只有頂點而沒有邊
有向圖和無向圖
有向圖
若圖G中的每條邊都是有方向的則稱G為有向圖(Digraph)
()有向邊的表示
在有向圖中一條有向邊是由兩個頂點組成的有序對有序對通常用尖括號表示有向邊也稱為弧(Arc)邊的始點稱為弧尾
(Tail)終點稱為弧頭(Head)
【例】表示一條有向邊v i 是邊的始點(起點)v j 是邊的終點因此和是兩條不
同的有向邊
()有向圖的表示
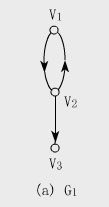
【例】下面(a)圖中G 是一個有向圖圖中邊的方向是用從始點指向終點的箭頭表示的該圖的頂點集和邊集分別為
V(G )={v v v }
E(G )={}
無向圖
若圖G中的每條邊都是沒有方向的則稱G為無向圖(Undigraph)
()無向邊的表示
無向圖中的邊均是頂點的無序對無序對通常用圓括號表示
【例】無序對(v i v j )和(v j v i )表示同一條邊
()無向圖的表示
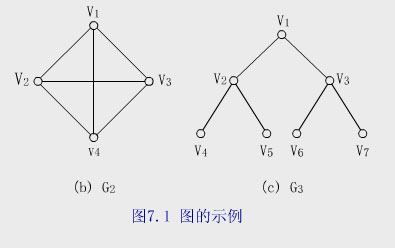
【例】下面(b)圖中的G 和(c)圖中的G 均是無向圖它們的頂點集和邊集分別為
V(G )={v v v v }
E(G )={(v l v )(v v )(v v )(v v )(v v )(v v )}
V(G )={v v v v v v v }
E(G )={(v v )(v l v )(v v )(v v )(v v )(v v )}
注意
在以下討論中不考慮頂點到其自身的邊即若(v v )或是E(G)中的一條邊則要求v ≠v 此外不允
許一條邊在圖中重復出現即只討論簡單的圖
圖G的頂點數n和邊數e的關系
()若G是無向圖則≤e≤n(n)/
恰有n(n)/條邊的無向圖稱無向完全圖(Undireeted Complete Graph)
()若G是有向圖則≤e≤n(n)
恰有n(n)條邊的有向圖稱為有向完全圖(Directed Complete Graph)
注意
完全圖具有最多的邊數任意一對頂點間均有邊相連
【例】上面(b)圖的G 就是具有個頂點的無向完全圖
From:http://tw.wingwit.com/Article/program/sjjg/201311/23860.html


