查找 - 線性表的查找 - 二分查找（二）

　　二分查找判定樹

　　二分查找過程可用二叉樹來描述把當前查找區間的中間位置上的結點作為根左子表和右子表中的結點分別作為根的左子樹和

　　右子樹由此得到的二叉樹稱為描述二分查找的判定樹(Decision Tree)或比較樹(Comparison Tree)

　　注意

　　判定樹的形態只與表結點個數n相關而與輸入實例中R[n]keys的取值無關

　　【例】具有個結點的有序表可用下圖所示的判定樹來表示

　　

　　()二分查找判定樹的組成

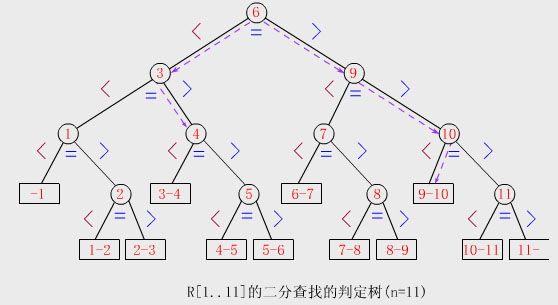
　　①圓結點即樹中的內部結點樹中圓結點內的數字表示該結點在有序表中的位置

　　②外部結點圓結點中的所有空指針均用一個虛擬的方形結點來取代即外部結點

　　③樹中某結點i與其左(右)孩子連接的左(右)分支上的標記<(>)表示當待查關鍵字

　　KR[i]key)時應走左(右)分支到達i的左(右)孩子將該孩子的關鍵字進一步和K比較若相等則查找過程結束返

　　回否則繼續將K與樹中更下一層的結點比較

　　()二分查找判定樹的查找

　　二分查找就是將給定值K與二分查找判定樹的根結點的關鍵字進行比較若相等成功否則若小於根結點的關鍵字到左子樹

　　中查找若大於根結點的關鍵字則到右子樹中查找

　　【例】對於有個結點的表若查找的結點是表中第個結點則只需進行一次比較;若查找的結點是表中第或第個結點則

　　需進行二次比較;找第個結點需要比較三次;找到第個結點需要比較四次

　　由此可見成功的二分查找過程恰好是走了一條從判定樹的根到被查結點的路徑經歷比較的關鍵字次數恰為該結點在樹中的層

　　數若查找失敗則其比較過程是經歷了一條從判定樹根到某個外部結點的路徑所需的關鍵字比較次數是該路徑上內部結點的總數

　　【例】待查表的關鍵字序列為()若要查找K=的記錄所經過的內部結點為

　　最後到達方形結點其比較次數為

　　實際上方形結點中ii+的含意為被查找值K是介於R[i]key和R[i+]key之間的即R[i]key

　　(3)二分查找的平均查找長度

　　設內部結點的總數為n=2 h -1，則判定樹是深度為h=lg(n+1)的滿二叉樹(深度h不計外部結點)。樹中第k層上的結點個數為2 k-

　　1 ，查找它們所需的比較次數是k。因此在等概率假設下，二分查找成功時的平均查找長度為：

　　ASL bn ≈lg(n+1)-1

　　二分查找在查找失敗時所需比較的關鍵字個數不超過判定樹的深度，在最壞情況下查找成功的比較次數也不超過判定樹的深度

　　。即為：

　　

　　二分查找的最壞性能和平均性能相當接近。

　　6、二分查找的優點和缺點

　　雖然二分查找的效率高，但是要將表按關鍵字排序。而排序本身是一種很費時的運算。既使采用高效率的排序方法也要花費

　　O(nlgn)的時間。

　　二分查找只適用順序存儲結構。為保持表的有序性，在順序結構裡插入和刪除都必須移動大量的結點。因此，二分查找特別適

　　用於那種一經建立就很少改動、而又經常需要查找的線性表。

　　對那些查找少而又經常需要改動的線性表，可采用鏈表作存儲結構，進行順序查找。鏈表上無法實現二分查找。

From:http://tw.wingwit.com/Article/program/sjjg/201311/23857.html