圖 - 最短路徑 （一）

　　帶權圖的最短路徑問題

　　帶權圖的最短路徑問題

　　帶權圖的最短路徑問題即求兩個頂點間長度最短的路徑

　　其中路徑長度不是指路徑上邊數的總和而是指路徑上各邊的權值總和

　　路徑長度的的具體含義取決於邊上權值所代表的意義

　　【例】交通網絡中常常提出的如下問題就是帶權圖中求最短路徑的問題

　　()兩地之間是否有路相通?

　　()在有多條通路的情況下哪一條最短?

　　其中:交通網絡可以用帶權圖表示圖中頂點表示城鎮邊表示兩個城鎮之間的道路邊上的權值可表示兩城鎮間的距離交通

　　費用或途中所需的時間等等

　　交通網絡的表示

　　由於交通網絡存在有向性所以一般以有向網絡表示交通網絡

　　【例】設A城到B城有一條公路A城的海拔高於B城若考慮到上坡和下坡的車速不同則邊和邊上表示行駛時間的權

　　值也不同即和應該是兩條不同的邊

　　源點和終點

　　習慣上稱路徑的開始頂點為源點(Source)路徑的最後一個頂點為終點(Destination)

　　為了討論方便設頂點集V={…n}並假定所有邊上的權值均是表示長度的非負實數

　　單源最短路徑問題

　　(SingleSource ShortestPathsProblem)

　　單源最短路徑問題已知有向帶權圖(簡稱有向網)G=(VE)找出從某個源點s∈V到V中其余各頂點的最短路徑

　　邊上權值相等的有向網的單源最短路徑

　　用求指定源點的BFS生成樹的算法可解決

　　迪傑斯特拉(Dijkstra)算法求單源最短路徑

　　由Dijkstra提出的一種按路徑長度遞增序產生各頂點最短路徑的算法

　　()按路徑長度遞增序產生各頂點最短路徑

　　若按長度遞增的次序生成從源點s到其它頂點的最短路徑則當前正在生成的最短路徑上除終點以外其余頂點的最短路徑均已生

　　成(將源點的最短路徑看作是已生成的源點到其自身的長度為的路徑)

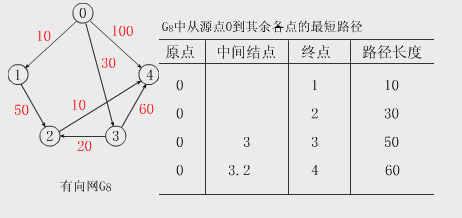
　　【例】在有向網G中假定以頂點為源點則它則其余各頂點的最短路徑按路徑遞增序排列如右表所示

　　

From:http://tw.wingwit.com/Article/program/sjjg/201311/23823.html