樹的路徑長度是從樹根到樹中每一結點的路徑長度之和
結點的權
結點的帶權路徑長度
樹的帶權路徑長度(Weighted Path Length of Tree)
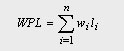
其中
n表示葉子結點的數目
w i 和l i 分別表示葉結點k i 的權值和根到結點k i 之間的路徑長度
樹的帶權路徑長度亦稱為樹的代價
在權為w l
哈夫曼樹
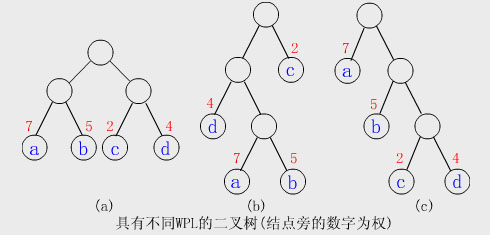
【例】給定
為
(a)WPL=
(b)WPL=
(c)WPL=
其中(c)樹的WPL最小
注意
① 葉子上的權值均相同時
② 最優二叉樹中
③ 最優二叉樹的形態不唯一
From:http://tw.wingwit.com/Article/program/sjjg/201311/23865.html
