樹 - 二叉樹 - 二叉樹的性質

　　二叉樹具有以下重要性質

　　性質 二叉樹第i層上的結點數目最多為 i (i≥)

　　證明 用數學歸納法證明

　　歸納基礎i=時有 i = =因為第層上只有一個根結點所以命題成立

　　歸納假設假設對所有的j(≤j

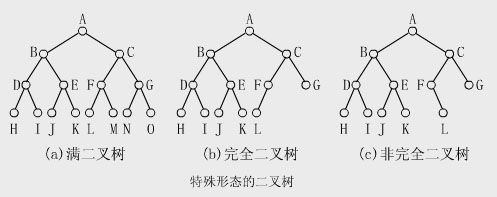
　　歸納步驟：根據歸納假設，第i-1層上至多有2 i-2 個結點。由於二叉樹的每個結點至多有兩個孩子，故第i層上的結點數至多是

　　第i-1層上的最大結點數的2倍。即j=i時，該層上至多有2×2 i-2 =2 i-1 個結點，故命題成立。

　　性質2 深度為k的二叉樹至多有2 k -1個結點(k≥1)。

　　證明 ：在具有相同深度的二叉樹中，僅當每一層都含有最大結點數時，其樹中結點數最多。因此利用性質1可得，深度為k的二叉樹

　　的結點數至多為：

　　2 0 +2 1 +…+2 k-1 =2 k -1

　　故命題正確。

　　性質3 在任意-棵二叉樹中，若終端結點的個數為n 0 ，度為2的結點數為n 2 ，則n o =n 2 +1。

　　證明 ：因為二叉樹中所有結點的度數均不大於2，所以結點總數(記為n)應等於0度結點數、1度結點(記為n 1 )和2度結點數之和：

　　n=n o +n 1 +n 2 (式子1)

　　另一方面，1度結點有一個孩子，2度結點有兩個孩子，故二叉樹中孩子結點總數是：

　　n l +2n 2

　　樹中只有根結點不是任何結點的孩子，故二叉樹中的結點總數又可表示為：

　　n=n 1 +2n 2 +1 (式子2)

　　由式子1和式子2得到：

　　n o =n 2 +1

　　滿二叉樹和完全二叉樹是二叉樹的兩種特殊情形。

　　1、滿二叉樹(FullBinaryTree)

　　一棵深度為k且有2 k -1個結點的二又樹稱為滿二叉樹。

　　滿二叉樹的特點：

　　(1) 每一層上的結點數都達到最大值。即對給定的高度，它是具有最多結點數的二叉樹。

　　(2) 滿二叉樹中不存在度數為1的結點，每個分支結點均有兩棵高度相同的子樹，且樹葉都在最下一層上。

　　【例】圖(a)是一個深度為4的滿二叉樹。

　　

　　2、完全二叉樹(Complete BinaryTree)

　　若一棵二叉樹至多只有最下面的兩層上結點的度數可以小於2，並且最下一層上的結點都集中在該層最左邊的若干位置上，則此二叉

　　樹稱為完全二叉樹。

　　特點：

　　(1) 滿二叉樹是完全二叉樹，完全二叉樹不一定是滿二叉樹。

　　(2) 在滿二叉樹的最下一層上，從最右邊開始連續刪去若干結點後得到的二叉樹仍然是一棵完全二叉樹。

　　(3) 在完全二叉樹中，若某個結點沒有左孩子，則它一定沒有右孩子，即該結點必是葉結點。

　　【例】如圖(c)中，結點F沒有左孩子而有右孩子L，故它不是一棵完全二叉樹。

　　【例】圖(b)是一棵完全二叉樹。

　　性質4 具有n個結點的完全二叉樹的深度為

　　

　　證明 ：設所求完全二叉樹的深度為k。由完全二叉樹定義可得：

　　深度為k得完全二叉樹的前k-1層是深度為k-1的滿二叉樹，一共有2 k-1 -1個結點。

　　由於完全二叉樹深度為k，故第k層上還有若干個結點，因此該完全二叉樹的結點個數：

　　n>2 k-1 -1。

　　另一方面，由性質2可得：

　　n≤2 k -1，

　　即：2 k-1 -l

　　由此可推出：2 k-1 ≤n<2 k ，取對數後有：

　　k-1≤lgn

　　又因k-1和k是相鄰的兩個整數，故有

　　

　　由此即得：

　　

　　注意：

　　

的證明【參見參考書目】

From:http://tw.wingwit.com/Article/program/sjjg/201311/23888.html