請按行及按列優先順序列出四維數組A***的所有元素在內存中的存儲次序開始結點為a
解
按行優先的順序排列時先變化右邊的下標也就是右到左依次變化這個四維數組的排列是這樣的(將這個排列分行寫出以便與閱讀只要按從左到右的順序存放就是在內存中的排列位置)
a a a
a a a
a a a
a a a
a a a
a a a
a a a
a a a
a a a
a a a
a a a
a a a
按列優先的順序排列恰恰相反變化最快的是左邊的下標然後向右變化所以這個四維數組的排列將是這樣的(這裡為了便於閱讀也將其書寫為分行形式)
a a
a a
a a
a a
a a
a a
a a
a a
a a
a a
a a
a a
a a
a a
a a
a a
a a
a a
給出C語言的三維數組地址計算公式
解
因為C語言的數組下標下界是所以
Loc(Amnp)=Loc(A)+((i*n*p)+k)*d
其中 Amnp表示三維數組Loc(A)表示數組起始位置ijk表示當前元素的下標d表示每個元素所占單元數
設有三對角矩陣 An*n將其三條對角線上的元素逐行地存儲到向量B[n]中使得B[k]=aij求
()用i j 表示k的下標變換公式
()用 k 表示 ij 的下標變換公式
() 解
要求ij 到k 的下標變換公式就是要知道在k之前已有幾個非零元素這些非零元素的個數就是k的值一個元素所在行為i所在列為j則在其前面已有的非零元素個數為
(i*)+j(i+)
其中 (i*)是這個元素前面所有行的非零元素個數j(i+)是它所在列前面的非零元素個數
化簡可得
k=i+j; // c下標是從開始的
() 解
因為K和ij是一一對應的關系因此這也不難算出
i=(k+)/ //k+表示當前元素前有幾個非零元素被整除就得到行號
j=(k+)%+(k+)/ //k+除以的余數就是表示當前行中第幾個非零元素
//加上前面的元素所點列數就是當前列號
設二維數組A*的每個元素占個字節已知Loc(a)=A共占多少個字節? A的終端結點a的起始地位為何?按行和按列優先存儲時a的起始地址分別為何?
解
()因含*=個元素因此A共占*=個字節
()a的起始地址為
Loc(a)=Loc(a)+(i*n+j)*d=+(*+)*=
()按行優先順序排列時
a=+(*+)*=
()按列優先順序排列時(二維數組可用行列下標互換來計算)
a=+(*+)*=
特殊矩陣和稀疏矩陣哪一種壓縮存儲後會失去隨機存取的功能?為什麼?
答
後者在采用壓縮存儲後將會失去隨機存儲的功能因為在這種矩陣中非零元素的分布是沒有規律的為了壓縮存儲就將每一個非零元素的值和它所在的行列號做為一個結點存放在一起這樣的結點組成的線性表中叫三元組表它已不是簡單的向量所以無法用下標直接存取矩陣中的元素
簡述廣義表和線性表的區別與聯系
答:
廣義表是線性表的推廣線性表是廣義表的特例當廣義表中的元素都是原子時即為線性表
畫出下列廣義表的圖形表示
() A(aB(bd)C(eB(bd)L(fg))) () A(aB(bA))
解:
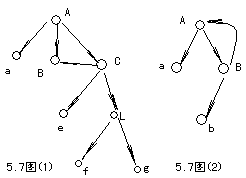
()這是一個再入表()則是一個遞歸表
設廣義表L=(()())試問head(L)tail(L)L的長度深度各為多少?
解
●head(L)=()
●tail(L)=(())
●L的長度為
●L的深度為
求下列廣義表運算的結果
()head ((phw)); ()tail((bkph)); () head (((ab)(cd)));
()tail(((ab)(cd))); ()head(tail(((ab)(cd))));
()tailhead)(((ab)(cd))))
答
()head ((phw))=p;
()tail((bkph))=(kph);
()head (((ab)(cd)))=(ab);
()tail(((ab)(cd)))=((cd));
()head(tail(((ab)(cd))))=(cd);
()tail(head(((ab)(cd))))=(b)
當三角矩陣采用題所述的壓縮存儲時寫一算法求三對角矩陣在這種壓縮存儲表示下的轉置矩陣
解
轉置矩陣就是將矩陣元素的行號與列號互換根據已知的三對角矩陣的特點其轉置矩陣對角線元素不變非零的非對角線元素aij與aji互換位置又知元素的下標和存放一維數組空間位置的關系k=i+j我們可以設計出這個矩陣的轉置算法
#define N //矩陣行列數
#define Length (*N)//壓縮矩陣的長度
typedef struct{
int data[Length];
}DiaMatrix;
void TransMatrix(DiaMatrix * C)
{ //壓縮三對角矩陣轉置
int i j;
int t;
for(i=; i<N;i++)
for(j=i; j<N; j++)
if(ij<=&&ij>=)
{ //將對應於行列號的壓縮矩陣內的元素互換
t=C>data[*i+j];
C>data[*i+j]=C>data[*j+i];
C>data[*j+i]=t;
}//endif
}//end
當稀疏矩陣A和B均以三元組表作為存儲結構時試寫出矩陣相加的算法其結果存放在三元組表C中
解
矩陣相加就是將兩個矩陣中同一位置的元素值相加由於兩個稀疏矩陣的非零元素按三元組表形式存放在建立新的三元組表C時為了使三元組元素仍按行優先排列所以每次插入的三元組不一定是A的按照矩陣元素的行列去找A中的三元組若有則加入C同時這個元素如果在B中也有則加上B的這個元素值否則這個值就不變;如果A中沒有則找B有則插入C無則查找下一個矩陣元素
#define MaxSize //用戶自定義
typedef int DataType; //用戶自定義
typedef struct
{ //定義三元組
int ij;
DataType v;
}TriTupleNode;
typedef struct
{ //定義三元組表
TriTupleNode data[MaxSize];
int mnt;//矩陣行列及三元組表長度
}TriTupleTable;
//以下為矩陣加算法
void AddTriTuple( TriTupl
From:http://tw.wingwit.com/Article/program/sjjg/201311/23887.html

