圖 - 最短路徑 （二）

　　()算法基本思想

　　設S為最短距離已確定的頂點集(看作紅點集)VS是最短距離尚未確定的頂點集(看作藍點集)

　　①初始化

　　初始化時只有源點s的最短距離是已知的(SD(s)=)故紅點集S={s}藍點集為空

　　②重復以下工作按路徑長度遞增次序產生各頂點最短路徑

　　在當前藍點集中選擇一個最短距離最小的藍點來擴充紅點集以保證算法按路徑長度遞增的次序產生各頂點的最短路徑

　　當藍點集中僅剩下最短距離為∞的藍點或者所有藍點已擴充到紅點集時s到所有頂點的最短路徑就求出來了

　　注意

　　①若從源點到藍點的路徑不存在則可假設該藍點的最短路徑是一條長度為無窮大的虛擬路徑

　　②從源點s到終點v的最短路徑簡稱為v的最短路徑;s到v的最短路徑長度簡稱為v的最短距離並記為SD(v)

　　()在藍點集中選擇一個最短距離最小的藍點k來擴充紅點集

　　根據按長度遞增序產生最短路徑的思想當前最短距離最小的藍點k的最短路徑是

　　源點紅點紅點…紅點n藍點k

　　距離為源點到紅點n最短距離+<紅點n藍點k>邊長

　　為求解方便設置一個向量D[n]對於每個藍點v∈ VS用D[v]記錄從源點s到達v且除v外中間不經過任何藍點(若有

　　中間點則必為紅點)的最短路徑長度(簡稱估計距離)

　　若k是藍點集中估計距離最小的頂點則k的估計距離就是最短距離即若D[k]=min{D[i] i∈VS}則D[k]=SD(k)

　　初始時每個藍點v的D[c]值應為權w且從s到v的路徑上沒有中間點因為該路徑僅含一條邊

　　注意

　　在藍點集中選擇一個最短距離最小的藍點k來擴充紅點集是Dijkstra算法的關鍵

　　()k擴充紅點集s後藍點集估計距離的修改

　　將k擴充到紅點後剩余藍點集的估計距離可能由於增加了新紅點k而減小此時必須調整相應藍點的估計距離

　　對於任意的藍點j若k由藍變紅後使D[j]變小則必定是由於存在一條從s到j且包含新紅點k的更短路徑P=且

　　D[j]減小的新路徑P只可能是由於路徑和邊組成

　　所以當length(P)=D[k]+w小於D[j]時應該用P的長度來修改D[j]的值

　　()Dijkstra算法

　　Dijkstra(GDs){

　　//用Dijkstra算法求有向網G的源點s到各頂點的最短路徑長度

　　//以下是初始化操作

　　S={s};D[s]=; //設置初始的紅點集及最短距離

　　for( all i∈ VS )do //對藍點集中每個頂點i

　　D[i]=G[s][i]; //設置i初始的估計距離為w

　　//以下是擴充紅點集

　　for(i=;i

　　D[k]=min{D[i]：all i V-S}; //在當前藍點集中選估計距離最小的頂點k

　　if(D[k]等於∞)

　　return; //藍點集中所有藍點的估計距離均為∞時，

　　//表示這些頂點的最短路徑不存在。Tw.WinGwiT.Com

　　S=S∪{k}; //將藍點k塗紅後擴充到紅點集

　　for( all j∈V-S )do //調整剩余藍點的估計距離

　　if(D[j]>D[k]+G[k][j])

　　//新紅點k使原D[j]值變小時，用新路徑的長度修改D[j]，

　　//使j離s更近。

　　D[j]=D[k]+G[k][j];

　　}

　　}

　　【例】對有向網G 8 以0為源點執行上述算法的過程及紅點集、k和D向量的變化見【 參見動畫演示 】。

　　

　　6)保存最短路徑的Dijkstra算法

　　設置記錄頂點雙親的向量P[0..n-1]保存最短路徑：

　　當頂點i無雙親時，令P[i]=-1。

　　當算法結束時，可從任一P[i]反復上溯至根(源點)求得頂點i的最短路徑，只不過路徑方向正好與從s到i的路徑相反。

　　具體的求精算法【參見教材】 。

　　Dijkstra算法的時間復雜度為O(n 2 )

　　其他最短路徑問題

　　最短路徑問題的提法很多，其它的最短路徑問題均可用單源最短路徑算法予以解決：

　　① 單目標最短路徑問題 (Single-Destination Shortest-Paths Problem)：找出圖中每一頂點v到某指定頂點u的最短路

　　徑。只需將圖中每條邊反向，就可將這一問題變為單源最短路徑問題，單目標u變為單源點u。

　　② 單頂點對間最短路徑問題 (Single-Pair Shortest-Path Problem)：對於某對頂點u和v，找出從u到v的一條最短路徑

　　。顯然，若解決了以u為源點的單源最短路徑問題，則上述問題亦迎刃而解。而且從數量級來說，兩問題的時間復雜度相同。

　　③ 所有頂點對間最短路徑問題 (All-Pairs Shortest-Paths Problem)：對圖中每對頂點u和v，找出u到v的最短路徑問題

　　。這一問題可用每個頂點作為源點調用一次單源最短路徑問題算法予以解決。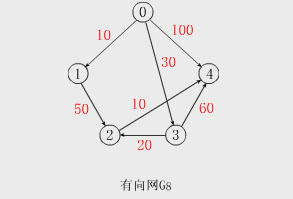

From:http://tw.wingwit.com/Article/program/sjjg/201311/23815.html