棧的應用實例

　　棧和隊列的應用非常之廣只要問題滿足後進先出和先進先出原則均可使用棧和隊列作為其數據結構

棧的應用

數制轉換
　　將一個非負的十進制整數N轉換為另一個等價的基為B的B進制數的問題很容易通過除B取余法來解決
　　【例】將十進制數轉化為二進制數
　　解答按除取余法得到的余數依次是則十進制數轉化為二進制數為
　　分析由於最先得到的余數是轉化結果的最低位最後得到的余數是轉化結果的最高位因此很容易用棧來解決

    　轉換算法如下
          typedef int DataType;//應將順序棧的DataType定義改為整型
          void MultiBaseOutput (int Nint B)
          {//假設N是非負的十進制整數輸出等值的B進制數
              int i;
              SeqStack S;
              InitStack(&S);
              while(N){  //從右向左產生B進制的各位數字並將其進棧
                    push(&SN%B); //將bi進棧<=i<=j
                    N=N/B;
              }
              while(!StackEmpty(&S)){  //棧非空時退棧輸出
                     i=Pop(&S);
                     printf(%di);
              }
            }
    　除數制的轉換外棧還可用於解決括號匹配檢查行編輯處理和表達式求解等問題具體【參見參考書目】

棧與遞歸
（） 遞歸
　　所謂遞歸是指若在一個函數過程或者數據結構定義的內部直接（或間接）出現定義本身的應用則稱它們是遞歸的或者是遞歸定義的
　　遞歸是一種強有力的數學工具它可使問題的描述和求解變得簡潔和清晰
　　遞歸算法常常比非遞歸算法更易設計尤其是當問題本身或所涉及的數據結構是遞歸定義的時候使用遞歸算法特別合適

（）遞歸算法的設計步驟
　　第一步驟（遞歸步驟）將規模較大的原問題分解為一個或多個規模更小但具有類似於原問題特性的子問題即較大的問題遞歸地用較小的子問題來描述解原問題的方法同樣可用來解這些子問題
　　第二步驟確定一個或多個無須分解可直接求解的最小子問題（稱為遞歸的終止條件）
　　【例】非負整數n的階乘可遞歸定義為

 
（）棧在遞歸算法的內部實現中所起的作用
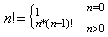
　　①調用函數時系統將會為調用者構造一個由參數表和返回地址組成的活動記錄並將其壓入到由系統提供的運行時刻棧的棧頂然後將程序的控制權轉移到被調函數若被調函數有局部變量則在運行時刻棧的棧頂也要為其分配相應的空間因此活動記錄和這些局部變量形成了一個可供被調函數使用的活動結構

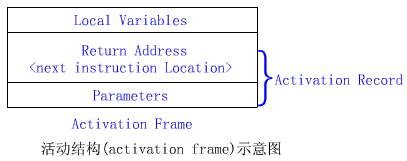
　注意
　　參數表的內容為實參返回地址是函數調用語句的下一指令的位置

　　②被調函數執行完畢時系統將運行時刻棧棧頂的活動結構退棧並根據退棧的活動結構中所保存的返回地址將程序的控制權轉移給調用者繼續執行
　　【例】Factorial（）遞歸函數執行期間運行時刻棧的變化（不考慮局部變量temp的入出棧情況）【參見動畫演示】

From:http://tw.wingwit.com/Article/program/sjjg/201311/22672.html