用Delphi編寫圓周率模擬器

圓周率π是個古老的東西早在多年前祖沖之已將其值精確到小數點後位而如今通過計算機程序已能算到十億位之多！我是個圓周率愛好者這個愛好至少是出於對這個無理數的熱衷我不但可以背誦到小數點後位而且還收藏著從網上找到幾個計算π的程序你有興趣可以到我的小站找一下
　　
　　一模擬器原理
　　
　　本程序並使用計算π值的算法她只是一個概率模擬即在邊長為的正方形內隨機產生多個點將點以圓弧為界分開統計由於點的個數很多直至幾乎布滿整個區域此時點的個數就可以看作就是它所在區域的面積可以得到如下推導
　　
　　藍色區內點個數總個數≈藍色面積總面積
　　藍色區內點個數總個數≈圓面積/總面積
　　藍色區內點個數總個數≈π××/×
　　π≈ ×藍色區內點個數/總個數
　　
　　當然點的位置會重復所以結果與π值是有差別的不過當點足夠多時可以看到一個非常接近的結果
　　
　　二程序設計
　　
　　打開Delphi 首先按照圖設計窗體
　　

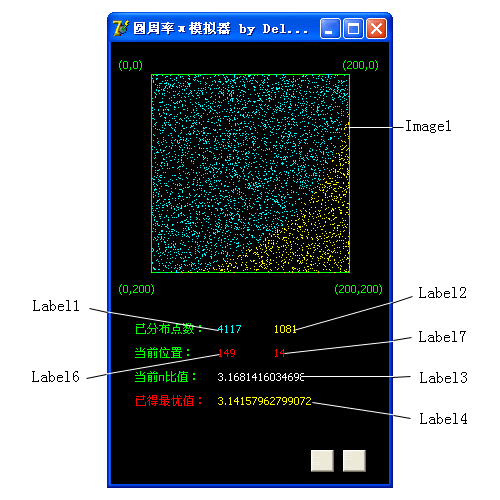
　　程序首先在Image控件區域內畫一個邊長為的正方形作為程序的演示窗口故FormCreate事件如下
　　
　　procedure TFormFormCreate(Sender: TObject);
　　begin
　　// 畫亮綠色的正方形演示框
　　ImageCanvasBrushColor:=clBlack;
　　ImageCanvasFillRect(Rect());
　　ImageCanvasPenColor:=cllime;
　　ImageCanvasRectangle();
　　DoubleBuffered := True;
　　end;
　　接著放入一個Timer實現點的繪制以及π的計算
　　
　　procedure TFormTimerTimer(Sender: TObject);
　　var
　　abiii:longint;
　　pipiok:single;
　　begin
　　// 隨機產生坐標點
　　i:=random();
　　ii:=random();
　　
　　if (i*i+ii*ii<) then
　　begin
　　// 以為半徑的圓內的點設為藍色
　　ImagecanvasPenColor:=claqua;
　　a:=StrToInt(LabelCaption);
　　LabelCaption:=IntToStr(a+);
　　//顯示當前點的坐標
　　LabelCaption:=IntToStr(ImageCanvasPenPosX);
　　LabelCaption:=IntToStr(ImageCanvasPenPosY);
　　end
　　else
　　begin
　　// 超出這個區域的點都在圓外設為黃色
　　ImageCanvasPenColor:=clyellow;
　　b:=StrToInt(LabelCaption);
　　LabelCaption:=IntToStr(b+);
　　end;
　　
　　// 畫點（長為像素的直線）
　　ImageCanvasMoveTo(iii);
　　ImageCanvasLineTo(iii+);
　　
　　// 計算pi的值
　　pi:=(*(StrToInt(LabelCaption))/(StrToInt(LabelCaption)+StrToInt(LabelCaption)));
　　LabelCaption:=FloatToStr(pi);
　　// Label顯示的是最接近真實pi的值
　　piok:=StrToFloat(LabelCaption);
　　//得出最接近的圓周率值 piok
　　if (abs(pi))<(abs(piok)) then
　　LabelCaption:=FloatToStr(pi);
　　end;
　　
　　最後加入兩個SpeedButton作為開始和暫停按鈕代碼分別是TimerEnabled:=true;和TimerEnabled:=false;好了程序這樣就完成了趕快按下F親自模擬一下π的計算吧！
　　
　　三小結
　　
　　雖然程序並沒有采用圓周率的算法但能通過隨機數對π進行逼近而由無數點描成的美妙圓弧讓我們歎為觀止
From:http://tw.wingwit.com/Article/program/Delphi/201311/24655.html