稀疏矩陣
設矩陣Amn中有s個非零元素若s遠遠小於矩陣元素的總數(即s<<m×n)則稱A為稀疏矩陣
稀疏矩陣的壓縮存儲
為了節省存儲單元可只存儲非零元素由於非零元素的分布一般是沒有規律的因此在存儲非零元素的同時還必須存儲非零元素所在的行號列號才能迅速確定一個非零元素是矩陣中的哪一個元素稀疏矩陣的壓縮存儲會失去隨機存取功能
其中每一個非零元素所在的行號列號和值組成一個三元組(ijaij)並由此三元組惟一確定
稀疏矩陣進行壓縮存儲通常有兩類方法順序存儲和鏈式存儲鏈式存儲方法【參見參考書目】
三元組表
將表示稀疏矩陣的非零元素的三元組按行優先(或列優先)的順序排列(跳過零元素)並依次存放在向量中這種稀疏矩陣的順序存儲結構稱為三元組表
注意
以下的討論中均假定三元組是按行優先順序排列的
【例】下圖(a)所示的稀疏矩陣A的三元組表表示見圖(b)
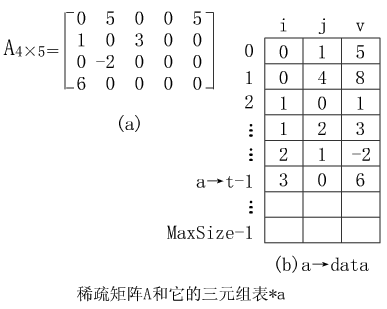
()三元組表的類型說明
為了運算方便將矩陣的總行數總列數及非零元素的總數均作為三元組表的屬性進行描述其類型描述為
#define MaxSize //由用戶定義
typedef int DataType //由用戶定義
typedef struct { //三元組
int ij//非零元的行列號
DataType v //非零元的值
}TriTupleNode
typedef struct{ //三元組表
TriTupleNode data[MaxSize] //三元組表空間
int mnt //矩陣的行數列數及非零元個數
}TriTupleTable
() 壓縮存儲結構上矩陣的轉置運算
一個m×n的矩陣A它的轉置矩陣B是一個n×m的矩陣且
A[i][j]=B[j][i]≤i<m≤j<n
即A的行是B的列A的列是B的行
【例】下圖中的B和上圖中的A互為轉置矩陣
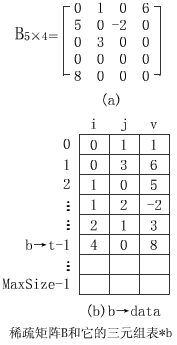
①三元組表表示的矩陣轉置的思想方法
第一步根據A矩陣的行數列數和非零元總數確定B矩陣的列數行數和非零元總數
第二步當三元組表非空(A矩陣的非零元不為)時根據A矩陣三元組表的結點空間data(以下簡稱為三元組表)將A的三元組表a>data置換為B的三元組表b>data
②三元組表的轉置
方法一:簡單地交換a>data中i和j中的內容得到按列優先順序存儲倒b>data;再將b>data重排成按行優先順序的三元組表
方法二:由於A的列是B的行因此按a>data的列序轉置所得到的轉置矩陣B的三元組表b>data必定是按行優先存放的
按這種方法設計的算法其基本思想是對A中的每一列col(≤col≤a>n)通過從頭至尾掃描三元組表a>data找出所有列號等於col的那些三元組將它們的行號和列號互換後依次放人b>data中即可得到B的按行優先的壓縮存貯表示具體實現參見【動畫演示】
③具體算法
void TransMatrix(TriTupleTable *bTriTupleTable *a)
{//*a*b是矩陣AB的三元組表表示求A轉置為B
int pqcol
b>m=a>n b>n=a>m //A和B的行列總數互換
b>t=a>t //非零元總數
if(b>t<=)
Error(A=) //A中無非零元退出
q=
for(col=col<a>ncol++) //對A的每一列
for(p=p<a>tp++) //掃描A的三元組表
if(a>data[p].j==col){ //找列號為col的三元組
b>data[q).i=a>data[p]j
b>data[q].j=a>data[p]i
b>data[q].v=a>data[p]v
q++
}
} //TransMatrix
④算法分析
該算法的時間主要耗費在col和p的二重循環上
若A的列數為n非零元素個數t則執行時間為O(n×t)即與A的列數和非零元素個數的乘積成正比
通常用二維數組表示矩陣時其轉置算法的執行時間是O(m×n)它正比於行數和列數的乘積
由於非零元素個數一般遠遠大於行數因此上述稀疏矩陣轉置算法的時間大於通常的轉置算法的時間
帶行表的三元組表
為了方便某些矩陣運算在按行優先存儲的三元組表中加入一個行表來記錄稀疏矩陣中每行的非零元素在三元組表中的起始位置這就是帶行表的三元組表
()類型描述
#define MaxRow l //在三元組表定義前加入此最大行定義
typedef struct {
TriTupleNode data[MaxSize]
int RowTab[MaxRow]//行表應保證m≤MaxRow
int mnt;
}RTriTupleTable
()帶行表的三元組表的操作
① 對於任給行號i(≤i≤m)能迅速地確定該行的第一個非零元在三元組表中的存儲位置為RowTab[i]
② RowTab[i](≤i≤m)表示第i行之前的所有行的非零元數
③ 第i行上的非零元數目為RowTab[i+]RowTab[i](≤i≤m)
④ 最後一行(即第ml行)的非零元數目為tRowTab[m](t為矩陣的非零元總數)
注意
若在行表中令RowTab[m]=t(要求MaxRow>m)會更方便 些且t可省略
帶行表的三元組表可改進矩陣的轉置算法具體【參閱其它參考書】
.稀疏矩陣壓縮存儲方式分析
() 三元組表和帶行表的三元組表的特點
相應的算法描述較為簡單但這類順序存儲方式對於非零元的位置或個數經常發生變化的矩陣運算就顯得不太適合
【例】執行將矩陣B相加到矩陣A上的運算時某位置上的結果可能會由非零元變為零元但也可能由零元變為非零元這就會引起在A的三元組表中進行刪除和插人操作從而導致大量結點的移動對此類運算采用鏈式存儲結構為宜
()稀疏矩陣的鏈式結構
稀疏矩陣的鏈式結構有十字鏈表等方法適用於非零元變化大的場合 比較復雜可【參閱其它參考書】
From:http://tw.wingwit.com/Article/program/sjjg/201311/23671.html


