稀疏矩陣
設矩陣A mn 中有s個非零元素 1、稀疏矩陣的壓縮存儲 為了節省存儲單元,可只存儲非零元素。由於非零元素的分布一般是沒有規律的,因此在存儲非零元素的同時,還必須存儲非零 元素所在的行號、列號,才能迅速確定一個非零元素是矩陣中的哪一個元素。稀疏矩陣的壓縮存儲會失去隨機存取功能。 其中每一個非零元素所在的行號、列號和值組成一個三元組(i,j,a ij ),並由此三元組惟一確定。 稀疏矩陣進行壓縮存儲通常有兩類方法:順序存儲和鏈式存儲。鏈式存儲方法【參見參考書目】。 2、三元組表 將表示稀疏矩陣的非零元素的三元組按行優先(或列優先)的順序排列(跳過零元素),並依次存放在向量中,這種稀疏矩陣的順序 存儲結構稱為三元組表。 注意: 以下的討論中,均假定三元組是按行優先順序排列的。 【例】下圖(a)所示的稀疏矩陣A的三元組表表示見圖(b)
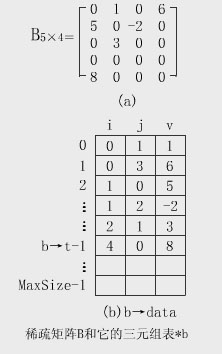
(1)三元組表的類型說明 為了運算方便,將矩陣的總行數、總列數及非零元素的總數均作為三元組表的屬性進行描述。Tw.wiNGwIT.Com其類型描述為: #define MaxSize 10000 //由用戶定義 typedef int DataType; //由用戶定義 typedef struct { //三元組 int i,j;//非零元的行、列號 DataType v; //非零元的值 }TriTupleNode; typedef struct{ //三元組表 TriTupleNode data[MaxSize]; //三元組表空間 int m,n,t; //矩陣的行數、列數及非零元個數 }TriTupleTable; (2) 壓縮存儲結構上矩陣的轉置運算 一個m×n的矩陣A,它的轉置矩陣B是一個n×m的矩陣,且: A[i][j]=B[j][i],0≤i 即A的行是B的列,A的列是B的行。 【例】下圖中的B和上圖中的A互為轉置矩陣。
①三元組表表示的矩陣轉置的思想方法 第一步:根據A矩陣的行數、列數和非零元總數確定B矩陣的列數、行數和非零元總數。 第二步:當三元組表非空(A矩陣的非零元不為0)時,根據A矩陣三元組表的結點空間data(以下簡稱為三元組表),將A的三 元組表a->data置換為B的三元組表b->data。 ②三元組表的轉置 方法一:簡單地交換a->data中i和j中的內容,得到按列優先順序存儲倒b->data;再將b->data重排成按行優先順序的三元組表。 方法二:由於A的列是B的行,因此,按a->data的列序轉置,所得到的轉置矩陣B的三元組表b->data必定是按行優先存放的。 按這種方法設計的算法,其基本思想是:對A中的每一列col(0≤col≤a->n-1),通過從頭至尾掃描三元組表a->data,找出所有 列號等於col的那些三元組,將它們的行號和列號互換後依次放人b->data中,即可得到B的按行優先的壓縮存貯表示。具體實現參見 【 動畫演示 】 ③具體算法: void TransMatrix(TriTupleTable *b,TriTupleTable *a) {//*a,*b是矩陣A、B的三元組表表示,求A轉置為B int p,q,col; b->m=a->n; b->n=a->m; //A和B的行列總數互換 b->t=a->t; //非零元總數 if(b->t<=0) Error("A=0"); //A中無非零元,退出 q=0; for(col=0;coln;col++) //對A的每一列 for(p=0;pt;p++) //掃描A的三元組表 if(a->data[p].j==col){ //找列號為col的三元組 b->data[q).i=a->data[p].j; b->data[q].j=a->data[p].i; b->data[q].v=a->data[p].v; q++; } } //TransMatrix ④算法分析 該算法的時間主要耗費在col和p的二重循環上: 若A的列數為n,非零元素個數t,則執行時間為O(n×t),即與A的列數和非零元素個數的乘積成正比。 通常用二維數組表示矩陣時,其轉置算法的執行時間是O(m×n),它正比於行數和列數的乘積。 由於非零元素個數一般遠遠大於行數,因此上述稀疏矩陣轉置算法的時間大於通常的轉置算法的時間。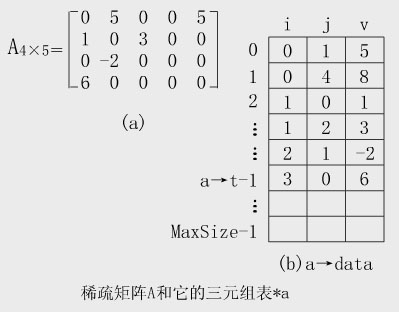
From:http://tw.wingwit.com/Article/program/sjjg/201311/23897.html
