()漸進時間復雜度評價算法時間性能
主要用算法時間復雜度的數量級(即算法的漸近時間復雜度)評價一個算法的時間性能
【例】有兩個算法A 和A 求解同一問題時間復雜度分別是T (n)=n T (n)=n
()當輸入量n<時有T (n)>T (n)後者花費的時間較少
()隨著問題規模n的增大兩個算法的時間開銷之比n /n =n/亦隨著增大即當問題規模較大時算法A 比算法A 要有效地多
它們的漸近時間復雜度O(n )和O(n )從宏觀上評價了這兩個算法在時間方面的質量在算法分析時往往對算法的時間復雜度和漸近時間復
雜度不予區分而經常是將漸近時間復雜度T(n)=O(f(n))簡稱為時間復雜度其中的f(n)一般是算法中頻度最大的語句頻度
【例】算法MatrixMultiply的時間復雜度一般為T(n)=O(n )f(n)=n 是該算法中語句()的頻度下面再舉例說明如何求算法的時間復
雜度
【例】交換i和j的內容
Temp=i;
i=j;
j=temp;
以上三條單個語句的頻度均為該程序段的執行時間是一個與問題規模n無關的常數算法的時間復雜度為常數階記作T(n)=O()
如果算法的執行時間不隨著問題規模n的增加而增長即使算法中有上千條語句其執行時間也不過是一個較大的常數此類算法的時間復雜度
是O()
【例】變量計數之一
() x=;y=;
() for(k;k<=n;k++)
() x++;
() for(i=;i<=n;i++)
() for(j=;j<=n;j++)
() y++;
一般情況下對步進循環語句只需考慮循環體中語句的執行次數忽略該語句中步長加終值判別控制轉移等成分因此以上程序段
中頻度最大的語句是()其頻度為f(n)=n 所以該程序段的時間復雜度為T(n)=O(n )
當有若干個循環語句時算法的時間復雜度是由嵌套層數最多的循環語句中最內層語句的頻度f(n)決定的
【例】變量計數之二
() x=;
() for(i=;i<=n;i++)
() for(j=;j<=i;j++)
() for(k=;k<=j;k++)
() x++;
該程序段中頻度最大的語句是()內循環的執行次數雖然與問題規模n沒有直接關系但是卻與外層循環的變量取值有關而最外層循環的
次數直接與n有關因此可以從內層循環向外層分析語句()的執行次數
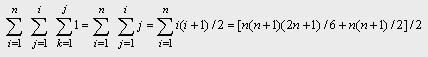
則該程序段的時間復雜度為T(n)=O(n /+低次項)=O(n )
()算法的時間復雜度不僅僅依賴於問題的規模還與輸入實例的初始狀態有關
【例】在數值A[n]中查找給定值K的算法大致如下
()i=n;
()while(i>=&&(A[i]!=k))
() i;
()return i;
此算法中的語句()的頻度不僅與問題規模n有關還與輸入實例中A的各元素取值及K的取值有關:
①若A中沒有與K相等的元素則語句()的頻度f(n)=n;
②若A的最後一個元素等於K則語句()的頻度f(n)是常數
()最壞時間復雜度和平均時間復雜度
最壞情況下的時間復雜度稱最壞時間復雜度一般不特別說明討論的時間復雜度均是最壞情況下的時間復雜度
這樣做的原因是最壞情況下的時間復雜度是算法在任何輸入實例上運行時間的上界這就保證了算法的運行時間不會比任何更長
【例】查找算法【例·】在最壞情況下的時間復雜度為T(n)=(n)它表示對於任何輸入實例該算法的運行時間不可能大於(n)
平均時間復雜度是指所有可能的輸入實例均以等概率出現的情況下算法的期望運行時間
常見的時間復雜度按數量級遞增排列依次為常數()對數階(log n)線形階(n)線形對數階(nlog n)平方階(n )立方階(n
)…k次方階(n k )指數階( n )顯然時間復雜度為指數階( n )的算法效率極低當n值稍大時就無法應用
類似於時間復雜度的討論一個算法的空間復雜度(Space Complexity)S(n)定義為該算法所耗費的存儲空間它也是問題規模n的函數漸近空
間復雜度也常常簡稱為空間復雜度算法的時間復雜度和空間復雜度合稱為算法的復雜度
From:http://tw.wingwit.com/Article/program/sjjg/201311/23401.html