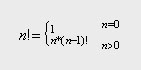棧與遞歸
() 遞歸
所謂 遞歸 是指若在一個函數過程或者數據結構定義的內部直接(或間接)出現定義本身的應用則稱它們是遞歸的或
者是遞歸定義的
遞歸是一種強有力的數學工具它可使問題的描述和求解變得簡潔和清晰
遞歸算法常常比非遞歸算法更易設計尤其是當問題本身或所涉及的數據結構是遞歸定義的時候使用遞歸算法特別合適
()遞歸算法的設計步驟
第一步驟(遞歸步驟) 將規模較大的原問題分解為一個或多個規模更小但具有類似於原問題特性的子問題即較大的問題遞
歸地用較小的子問題來描述解原問題的方法同樣可用來解這些子問題
第二步驟 確定一個或多個無須分解可直接求解的最小子問題(稱為 遞歸的終止條件 )
【例】非負整數n的階乘可遞歸定義為
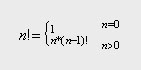
()棧在遞歸算法的內部實現中所起的作用
①調用函數時系統將會為調用者構造一個由參數表和返回地址組成的活動記錄並將其壓入到由系統提供的運行時刻棧的棧
頂然後將程序的控制權轉移到被調函數若被調函數有局部變量則在運行時刻棧的棧頂也要為其分配相應的空間因此活動記
錄和這些局部變量形成了一個可供被調函數使用的活動結構
注意
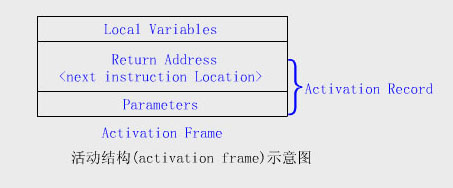
參數表的內容為實參返回地址是函數調用語句的下一指令的位置
②被調函數執行完畢時系統將運行時刻棧棧頂的活動結構退棧並根據退棧的活動結構中所保存的返回地址將程序的控制權
轉移給調用者繼續執行
【例】Factorial()遞歸函數執行期間運行時刻棧的變化(不考慮局部變量temp的入出棧情況)
From:http://tw.wingwit.com/Article/program/sjjg/201311/23918.html