多維數組-矩陣的壓縮存儲-特殊矩陣

　　特殊矩陣

　　所謂特殊矩陣是指非零元素或零元素的分布有一定規律的矩陣常見的有對稱矩陣三角矩陣和對角矩陣等

　　對稱矩陣

　　()對稱矩陣

　　在一個n階方陣A中若元素滿足下述性質

　　a ij =a ji ≤ij≤n

　　則稱A為對稱矩陣

　　【例】下圖便是一個階對稱矩陣

　　

　　()對稱矩陣的壓縮存儲

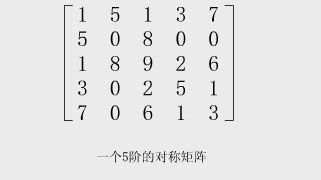
　　對稱矩陣中的元素關於主對角線對稱故只要存儲矩陣中上三角或下三角中的元素讓每兩個對稱的元素共享一個存儲空間這樣

　　能節約近一半的存儲空間

　　①按行優先順序存儲主對角線(包括對角線)以下的元素

　　

　　即按a a a ……a n a n …a nn 次序存放在一個向量sa[n(n+)/]中(下三角矩陣

　　中元素總數為n(n+)/)

　　其中

　　sa[]= a

　　sa[] = a

　　……

　　sa[n(n+)/]= a nn

　　②元素a ij 的存放位置

　　a ij 元素前有i行(從第行到第i行)一共有

　　++…+i=i×(i+)/個元素;

　　在第i行上aij之前恰有j個元素(即a i a il …a ij )因此有

　　sa[i×(i+)/+j]= a ij

　　③a ij 和sa[k]之間的對應關系

　　若i≥jk=i×(i+)/+j ≤k

　　若i

　　令I=max(i，j)，J=min(i，j)，則k和i，j的對應關系可統一為：

　　k=i×(i+1)/2+j 0≤k

　　(3)對稱矩陣的地址計算公式

　　LOC(a ij )=LOC(sa[k])

　　=LOC(sa[0])+k×d=LOC(sa[0])+[I×(I+1)/2+J]×d

　　通過下標變換公式，能立即找到矩陣元素a ij 在其壓縮存儲表示sa中的對應位置k。TW.WInGWIT.cOm因此是隨機存取結構。

　　【例】a 21 和a 12 均存儲在sa[4]中，這是因為

　　k=I×(I+1)/2+J=2×(2+1)/2+1=4

From:http://tw.wingwit.com/Article/program/sjjg/201311/23900.html