樹(自由樹)無序樹和有根樹
自由樹 就是一個無回路的連通圖(沒有確定根)(在自由樹中選定一頂點做根則成為一棵通常的樹)
從根開始為每個頂點(在樹中通常稱作結點)的孩子規定從左到右的次序則它就成為一棵 有序樹
在圖的應用中我們常常需要求給定圖的一個子圖使該子圖是一棵樹
生成樹
生成樹
如果連通圖G的一個子圖是一棵包含G的所有頂點的樹則該子圖稱為G的生成樹(SpanningTree)
生成樹是連通圖的包含圖中的所有頂點的極小連通子圖
圖的生成樹不惟一從不同的頂點出發進行遍歷可以得到不同的生成樹
深度優先生成樹和廣度優先生成樹
()生成樹的求解方法
設圖G=(VE)是一個具有n個頂點的連通圖則從G的任一頂點(源點)出發作一次深度優先搜索(廣度優先搜索)搜索到的
n個頂點和搜索過程中從一個已訪問過的頂點v i 搜索到一個未曾訪問過的鄰接點v j 所經過的邊(v i v j )(共n條)組成
的極小連通子圖就是生成樹(源點是生成樹的根)
通常由深度優先搜索得到的生成樹稱為深度優先生成樹簡稱為DFS生成樹;由廣度優先搜索得到的生成樹稱為廣度優先生成樹
簡稱為BPS生成樹
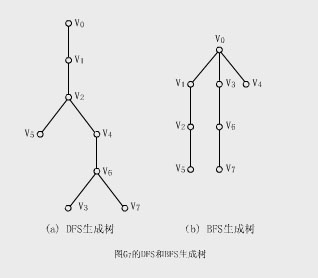
【例】從圖G 的頂點v 出發所得的DFS生成樹如下圖(a)具體生成過程【 參見動畫演示 】BFS生成樹如下圖(b)具
體生成過程【 參見動畫演示 】
()求DFS生成樹和BFS生成樹算法
只要在DFS(或DFSM)算法的if語句中在遞歸調用語句之前加入適當生成邊(v i v j )的操作(如將該邊輸出或保存)即可得到
求DFS生成樹的算法
在BFS(或BFSM)算法的if語句中加入生成樹邊(v i v j )的操作可得到求BFS生成樹的算法【參見練習】
注意
①圖的廣度優先生成樹的樹高不會超過該圖其它生成樹的高度
②圖的生成樹不惟一從不同的頂點出發進行遍歷可以得到不同的生成樹
生成樹的通用定義
若從圖的某頂點出發可以系統地訪問到圖中所有頂點則遍歷時經過的邊和圖的所有頂點所構成的子圖稱作該圖的生成樹(此
定義不僅僅適用於無向圖對有向圖同樣適用)
()若G是強連通的有向圖則從其中任一頂點v出發都可以訪問遍G中的所有頂點從而得到以v為根的生成樹
()若G是有根的有向圖設根為v則從根v出發可以完成對G的遍歷得到G的以v為根的生成樹
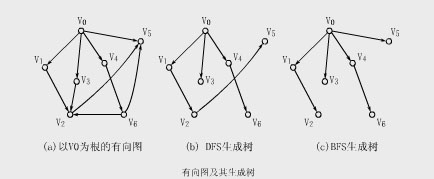
【例】下圖中(a)圖是以v 為根的有向圖它的DFS生成樹和BPS生成樹分別如圖(b)和(c)所示
()若G是非連通的無向圖則要若干次從外部調用DFS(或BFS)算法才能完成對G的遍歷每一次外部調用只能訪問到G的一個
連通分量的頂點集這些頂點和遍歷時所經過的邊構成了該連通分量的一棵DFS(或BPS)生成樹G的各個連通分量的DFS(或BFS)生成
樹組成了G的DFS(或BFS)生成森林
()若G是非強連通的有向圖且源點又不是有向圖的根則遍歷時一般也只能得到該有向圖的生成森林
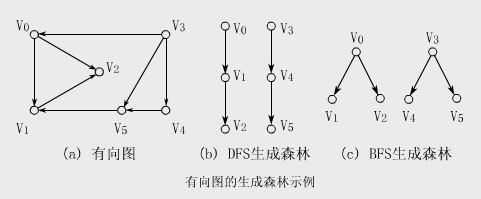
【例】下圖(a)所示的有向圖其DFS和BFS生成森林分別如(b)和(c)所示
From:http://tw.wingwit.com/Article/program/sjjg/201311/23831.html



