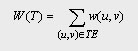最小生成樹
對於連通的帶權圖(連通網)G其生成樹也是帶權的生成樹T各邊的權值總和稱為該樹的權記作
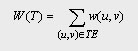
這裡:
TE表示T的邊集
w(uv)表示邊(uv)的權
權最小的生成樹稱為G的最小生成樹(Minimum SpannirngTree)最小生成樹可簡記為MST
生成樹和最小生成樹的應用
生成樹和最小生成樹有許多重要的應用
【例】網絡G表示n各城市之間的通信線路網線路(其中頂點表示城市邊表示兩個城市之間的通信線路邊上的權值表示線路的長度
或造價可通過求該網絡的最小生成樹達到求解通信線路或總代價最小的最佳方案
最小生成樹性質(MST性質)
()MST性質
最小生成樹性質設G=(VE)是一個連通網絡U是頂點集V的一個真子集若(uv)是G中所有的一個端點在U(u∈U)裡另一個端
點不在U(即v∈VU)裡的邊中具有最小權值的一條邊則一定存在G的一棵最小生成樹包括此邊(uv)
()MST性質的證明
為方便說明先作以下約定
①將集合U中的頂點看作是紅色頂點②而VU中的頂點看作是藍色頂點③連接紅點和藍點的邊看作是紫色邊④權最小的紫
邊稱為輕邊(即權重最輕的邊)於是MST性質中所述的邊(uv)就可簡稱為輕邊
用反證法證明MST性質
假設G中任何一棵MST都不含輕邊(uv)則若T是G的一棵MST則它不含此輕邊
由於T是包含了G中所有頂點的連通圖所以T中必有一條從紅點u到藍點v的路徑P且P上必有一條紫邊(uv)連接紅點集和藍點集
否則u和v不連通當把輕邊(uv)加入樹T時該輕邊和P必構成了一個回路刪去紫邊(uv)後回路亦消除由此可得另一生
成樹T
T和T的差別僅在於T用輕邊(uv)取代了T中權重可能更大的紫邊(uv)因為w(uv)≤w(uv)所以
w(T)=w(T)+w(uv)w(uv)≤w(T)
故T亦是G的MST它包含邊(uv)這與假設矛盾
所以MST性質成立
求MST的一般算法描述
求MST的一般算法可描述為針對圖G從空樹T開始往集合T中逐條選擇並加入n條安全邊(uv)最終生成一棵含n條邊的
MST
當一條邊(uv)加入T時必須保證T∪{(uv)}仍是MST的子集我們將這樣的邊稱為T的安全邊
用偽代碼可將算法描述為
GenerieMST(G){//求G的某棵MST
T〈¢; //T初始為空是指頂點集和邊集均空
while T未形成G的生成樹 do{
找出T的一條安全邊(uv);//即T∪{(uv)}仍為MST的子集
T=T∪{(uv)}; //加入安全邊擴充T
}
return T; //T為生成樹且是G的一棵MST
}
注意
下面給出的兩種求MST的算法均是對上述的一般算法的求精兩算法的區別僅在於求安全邊的方法不同
為簡單起見下面用序號…n來表示頂點集即
V(G)={…n}
G中邊上的權解釋為長度並設T=(UTE)
From:http://tw.wingwit.com/Article/program/sjjg/201311/23829.html