圖 - 生成樹和最小生成樹 - 最小生成樹（二）

　　普裡姆(Prim)算法

　　()算法思想

　　T=(UTE)是存放MST的集合

　　①T的初值是({r}￠)

　　即最小生成樹初始時只有一個紅點r沒有紅邊

　　②T經過n次如下步驟操作最後得到一棵含n個頂點n條邊的最小生成樹

　　⒈選擇紫邊集中一條輕邊並擴充進T

　　⒉將輕邊連接的藍點改紅點

　　⒊將輕邊改紅邊

　　⒋修改紫邊集

　　()較小紫邊集的構造

　　若當前形成的T中有k個頂點|U|=k|Vu|=nk故可能的紫邊數目是k(nk)從如此大的紫邊集中選擇輕邊是低效的因此

　　必須構造較小的紫邊集

　　對於每個藍點v ∈VU從v到各紅點的紫邊中只有最短的那一條才有可能是輕邊因此只須保留所有nk個藍點所關聯的最

　　短紫邊作為輕邊的候選集即可

　　()候選紫邊集合的修改

　　當把輕邊(uv)擴充到T時因為v由藍變紅故對每個剩余的藍點j邊(vj)就由非紫邊變為紫邊這條新紫邊的長度可能小

　　於藍點j原來所關聯的最短紫邊的長度因此用長度更小的新紫邊取代那些原有的最短紫邊

　　()Prim算法的偽代碼描述

　　PrimMST(GTr){

　　//求圖G的以r為根的MST結果放在T=(UTE)中

　　InitCandidateSet(…);//初始化設置初始的輕邊候選集並置T=({r}￠)

　　for(k=;k

　　(u，v)=SelectLiShtEdge(…);//選取輕邊(u，v);

　　T←T∪{(u，v)};//擴充T，即(u，v)塗紅加入TE，藍點v並人紅點集U

　　ModifyCandidateSet(…); //根據新紅點v調整候選輕邊集

　　}

　　}

　　(5) 算法的執行過程

　　用PRIM算法得到最小生成樹的過程【 參見動畫演示 】

　　

　　注意：

　　若候選輕邊集中的輕邊不止一條，可任選其中的一條擴充到T中。TW.WINgWIT.cOM

　　連通網的最小生成樹不一定是惟一的，但它們的權相等。

　　【例】在上圖(e)中，若選取的輕邊是(2，4)而不是(2，1)時，則得到如圖(h)所示的另一棵MST。

　　(6)算法特點

　　該算法的特點是當前形成的集合T始終是一棵樹。將T中U和TE分別看作紅點和紅邊集，V-U看作藍點集。算法的每一步均是在連接

　　紅、藍點集的紫邊中選擇一條輕邊擴充進T中。MST性質保證了此邊是安全的。T從任意的根r開始，並逐漸生長直至U=V，即T包含了

　　C中所有的頂點為止。MST性質確保此時的T是G的一棵MST。因為每次添加的邊是使樹中的權盡可能小，因此這是一種"貪心"的策略。

　　(7)算法分析

　　該算法的時間復雜度為O(n 2 )。與圖中邊數無關，該算法適合於稠密圖。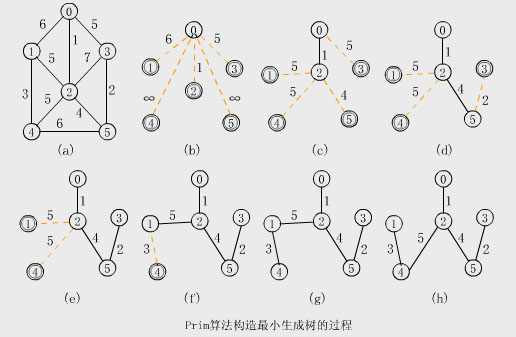

From:http://tw.wingwit.com/Article/program/sjjg/201311/23827.html