圖 - 生成樹和最小生成樹 - 最小生成樹（三）

　　克魯斯卡爾(Kruskal)算法

　　()算法思想

　　①T的初始狀態

　　只有n個頂點而無邊的森林T=(V￠ )

　　②按邊長遞增的順序選擇E中的n安全邊(uv)並加入T生成MST

　　注意

　　安全邊指兩個端點分別是森林T裡兩棵樹中的頂點的邊加入安全邊可將森林中的兩棵樹連接成一棵更大的樹

　　因為每一次添加到T中的邊均是當前權值最小的安全邊MST性質也能保證最終的T是一棵最小生成樹

　　()算法特點

　　該算法的特點是當前形成的集合T除最後的結果外始終是一個森林

　　()Kruskal算法的抽象描述

　　KruskalMST(G){//求連通網G的一棵MST

　　T=(V￠); //初始化T是只含n個頂點不包含邊的森林

　　依權值的遞增序對E(G)中的邊排序並設結果在E[e]中

　　for(i=;i

　　取E[0..e-1)中的第i條邊(u，v);

　　if u和v分別屬於T中兩棵不同的樹then

　　T=T∪{(u，v)};//(u，v)是安全邊，將其加入T中

　　if T已是一棵生成樹then

　　`` return T;

　　}//endfor

　　return T;

　　}

　　(4)用Kruskal算法構造最小生成樹的過程

　　用Kruskal算法構造最小生成樹的過程【 參見動畫演示 】

　　

　　(5)算法分析

　　該算法的時間復雜度為O(elge)。TW.wiNGwIT.CoM

　　Kruskal算法的時間主要取決於邊數。它較適合於稀疏圖。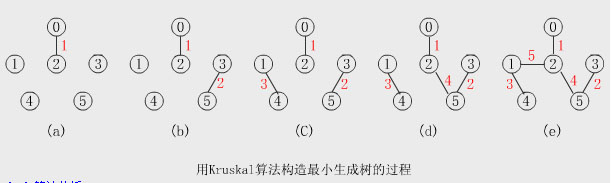

From:http://tw.wingwit.com/Article/program/sjjg/201311/23825.html