)在二叉排序樹上進行查找時的平均查找長度和二叉樹的形態有關
二分查找法查找長度為n的有序表其判定樹是惟一的含有n個結點的二叉排序樹卻不惟一對於含有同樣一組結點的表由於
結點插入的先後次序不同所構成的二叉排序樹的形態和深度也可能不同
【例】下圖(a)所示的樹是按如下插入次序構成的
下圖(b)所示的樹是按如下插入次序構成的
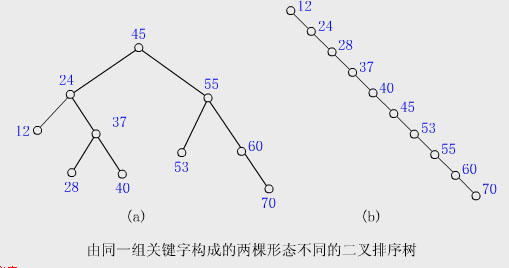
在二叉排序樹上進行查找時的平均查找長度和二叉樹的形態有關
①在最壞情況下二叉排序樹是通過把一個有序表的n個結點依次插入而生成的此時所得的二叉排序樹蛻化為棵深度為n的單支
樹它的平均查找長度和單鏈表上的順序查找相同亦是(n+)/
②在最好情況下二叉排序樹在生成的過程中樹的形態比較勻稱最終得到的是一棵形態與二分查找的判定樹相似的二叉排序
樹此時它的平均查找長度大約是lgn
③插入刪除和查找算法的時間復雜度均為O(lgn)
()二叉排序樹和二分查找的比較
就平均時間性能而言二叉排序樹上的查找和二分查找差不多
就維護表的有序性而言二叉排序樹無須移動結點只需修改指針即可完成插入和刪除操作且其平均的執行時間均為O(lgn)
因此更有效二分查找所涉及的有序表是一個向量若有插入和刪除結點的操作則維護表的有序性所花的代價是O(n)當有序表是
靜態查找表時宜用向量作為其存儲結構而采用二分查找實現其查找操作;若有序表裡動態查找表則應選擇二叉排序樹作為其存
儲結構
()平衡二叉樹
為了保證二叉排序樹的高度為lgn從而保證然二叉排序樹上實現的插入刪除和查找等基本操作的平均時間為O(lgn)在往樹
中插入或刪除結點時要調整樹的形態來保持樹的平衡使之既保持BST性質不變又保證樹的高度在任何情況下均為O(lgn)從而
確保樹上的基本操作在最壞情況下的時間均為O(lgn)
注意
①平衡二叉樹(Balanced Binary Tree)是指樹中任一結點的左右子樹的高度大致相同
②任一結點的左右子樹的高度均相同(如滿二叉樹)則二叉樹是完全平衡的通常只要二叉樹的高度為O(gn)就可看作是平
衡的
③平衡的二叉排序樹指滿足BST性質的平衡二叉樹
④AVL樹中任一結點的左右子樹的高度之差的絕對值不超過在最壞情況下n個結點的AVL樹的高度約為lgn而完全平
衡的二叉樹度高約為lgnAVL樹是接近最優的
From:http://tw.wingwit.com/Article/program/sjjg/201311/23811.html

