當查找的文件較大
B
一棵m(m≥
(
(j
其中
j為關鍵字總數
K i ( P i (0≤i≤j)是孩子指針。對於葉結點,每個P i 為空指針。 注意: ①實用中為節省空間,葉結點中可省去指針域P i ,但必須在每個結點中增加一個標志域leaf,其值為真時表示葉結點,否則為 內部結點。 ②在每個內部結點中,假設用keys(Pi)來表示子樹Pi中的所有關鍵字,則有: keys(P 0 ) 即關鍵字是分界點,任一關鍵字Ki左邊子樹中的所有關鍵字均小於K i ,右邊子樹中的所有關鍵字均大於K i 。 (2)所有葉子是在同一層上,葉子的層數為樹的高度h。 (3)每個非根結點中所包含的關鍵字個數j滿足:
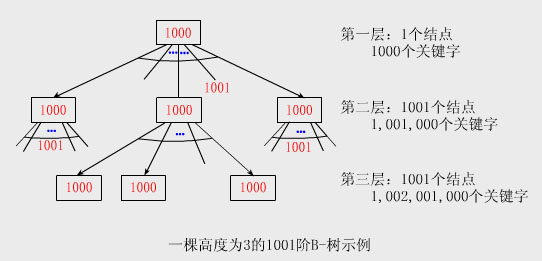
(4)若樹非空,則根至少有1個關鍵字,故若根不是葉子,則它至少有2棵子樹。根至多有m-1個關鍵字,故至多有m棵子樹。 2、B-樹的結點規模 在大多數系統中,B-樹上的算法執行時間主要由讀、寫磁盤的次數來決定,每次讀寫盡可能多的信息可提高算法得執行速度。 B-樹中的結點的規模一般是一個磁盤頁,而結點中所包含的關鍵字及其孩子的數目取決於磁盤頁的大小。 注意: ①對於磁盤上一棵較大的B-樹,通常每個結點擁有的孩子數目(即結點的度數)m為50至2000不等 ②一棵度為m的B-樹稱為m階B-樹。 ③選取較大的結點度數可降低樹的高度,以及減少查找任意關鍵字所需的磁盤訪問次數。 【例】下圖給出了一棵高度為3的1001階B-樹。
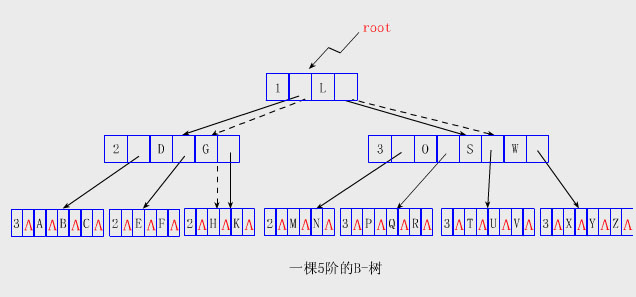
說明: ①每個結點包含1000個關鍵字,故在第三層上有100多萬個葉結點,這些葉節點可容納10億多個關鍵字。 ②圖中各結點內的數字表示關鍵字的數目。 ③通常根結點可始終置於主存中,因此在這棵B-樹中查找任一關鍵字至多只需二次訪問外存。 3、B-樹的存儲結構 #define Max l000 //結點中關鍵字的最大數目:Max=m-1,m是B-樹的階 #define Min 500 //非根結點中關鍵字的最小數目:Min=┌m/2┐-1 typedef int KeyType; //KeyType應由用戶定義 typedef struct node{ //結點定義中省略了指向關鍵字代表的記錄的指針 int keynum; //結點中當前擁有的關鍵字的個數,keynum《Max KeyType key[Max+1]; //關鍵字向量為key[1..keynum],key[0]不用。 struct node *parent; //指向雙親結點 struct node *son[Max+1];//孩子指針向量為son[0..keynum] }BTreeNode; typedef BTreeNode *BTree; 注意: 為簡單起見,以上說明省略了輔助信息域。在實用中,與每個關鍵字存儲在一起的不是相關的輔助信息域,而是一個指向另一磁 盤頁的指針。磁盤頁中包含有該關鍵字所代表的記錄,而相關的輔助信息正是存儲在此記錄中。 有的B-樹(如第10章介紹的B+樹)是將所有輔助信息都存於葉結點中,而內部結點(不妨將根亦看作是內部結點)中只存放關鍵字和 指向孩子結點的指針,無須存儲指向輔助信息的指針,這樣使內部結點的度數盡可能最大化。 4、5階B-樹示例 【例】下圖給出了一棵包含24個英文字母的5階B-樹的存儲結構圖。
說明: 按照定義,在5階B-樹裡,根中的關鍵字數目可以是1~4,子樹數可以是2~5;其它的結點中關鍵字數目可以是2~4,若該結點 不是葉子,則它可以有3~5棵子樹。 B-樹上的基本運算 1、B-樹的查找 (1)B-樹的查找方法 在B-樹中查找給定關鍵字的方法類似於二叉排序樹上的查找。不同的是在每個結點上確定向下查找的路徑不一定是二路而是 keynum+1路的。 對結點內的存放有序關鍵字序列的向量key[l..keynum] 用順序查找或折半查找方法查找。若在某結點內找到待查的關鍵字K,則 返回該結點的地址及K在key[1..keynum]中的位置;否則,確定K在某個key[i]和key[i+1]之間結點後,從磁盤中讀son[i]所指的 結點繼續查找……。直到在某結點中查找成功;或直至找到葉結點且葉結點中的查找仍不成功時,查找過程失敗。 【例】下圖中左邊的虛線表示查找關鍵字1的過程,它失敗於葉結點的H和K之間空指針上;右邊的虛線表示查找關鍵字S的過程,並成 功地返回S所在結點的地址和S在key[1..keynum]中的位置2。
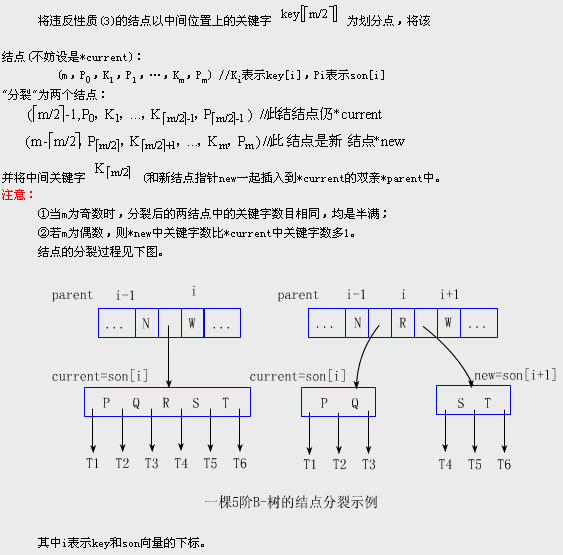
(2)B-樹的查找算法 BTreeNode *SearchBTree(BTree T,KeyType K,int *pos) { //在B-樹T中查找關鍵字K,成功時返回找到的結點的地址及K在其中的位置*pos //失敗則返回NULL,且*pos無定義 int i; T→key[0]=k; //設哨兵.下面用順序查找key[1..keynum] for(i=T->keynum;K if(i>0 && T->key[i]==1){ //查找成功,返回T及i *pos=i; return T; } //結點內查找失敗,但T->key[i] //son[i] if(!T->son[i]) //*T為葉子,在葉子中仍未找到K,則整個查找過程失敗 return NULL; //查找插入關鍵字的位置,則應令*pos=i,並返回T,見後面的插入操作 DiskRead(T->son[i]); //在磁盤上讀人下一查找的樹結點到內存中 return SearchBTree(T->Son[i],k,pos); //遞歸地繼續查找於樹T->son[i] (3)查找操作的時間開銷 B-樹上的查找有兩個基本步驟: ①在B-樹中查找結點,該查找涉及讀盤DiskRead操作,屬外查找; ②在結點內查找,該查找屬內查找。 查找操作的時間為: ①外查找的讀盤次數不超過樹高h,故其時間是O(h); ②內查找中,每個結點內的關鍵字數目keynum 注意: ①實際上外查找時間可能遠遠大於內查找時間。 ②B-樹作為數據庫文件時,打開文件之後就必須將根結點讀人內存,而直至文件關閉之前,此根一直駐留在內存中,故查找時 可以不計讀入根結點的時間。 2、B-樹的插入和生成 B-樹的生成是從空樹起,逐個插入關鍵字而得到的。 (1)插入關鍵字K的方法 首先在樹中查找K,若找到則直接返回(假設不處理相同關鍵字的插入);否則查找操作必失敗於某個葉子上,然後將K插入該葉子 中。若該葉子結點原來是非滿(指keynum 即完成了插入操作;若該結點原為滿,則K插入後keynum=m,違反B-樹性質(3),故須調整使其維持B-樹性質不變。 調整操作:
注意: 當
均是滿結點,此時,插入過程中的分裂操作一直向上傳播到根。當根分裂時,因根沒有雙親,故需建立一個新的根,此時樹長高一層 。 (2)B-樹的生成 由空樹開始,逐個插入關鍵字,即可生成B-樹。 【例】以關鍵字序列(a,g,f,b,k,d,h,m,i,e, s,i,r,x,c,l,n,t,u,p)建立一棵5階B-樹的生長過程 注意: ①當一結點分裂時所產生的兩個結點大約是半滿的,這就為後續的插入騰出了較多的空間,尤其是當m較大時,往這些半滿的空間 中插入新的關鍵字不會很快引起新的分裂。 ②向上插人的關鍵字總是分裂結點的中間位置上的關鍵字,它未必是正待插入該分裂結點的關鍵字。因此,無論按何次序插入關 鍵字序列,樹都是平衡的。 3、B-樹的刪除 (1)刪除操作的兩個步驟 第一<


![]()
From:http://tw.wingwit.com/Article/program/sjjg/201311/23807.html
