() BuildHeap和Heapify函數的實現
因為構造初始堆必須使用到調整堆的操作先討論Heapify的實現
① Heapify函數思想方法
每趟排序開始前R[li]是以R[]為根的堆在R[]與R[i]交換後新的無序區R[i]中只有R[]的值發生了變化故除
R[]可能違反堆性質外其余任何結點為根的子樹均是堆因此當被調整區間是R[lowhigh]時只須調整以R[low]為根的樹即
可
篩選法調整堆
R[low]的左右子樹(若存在)均已是堆這兩棵子樹的根R[low]和R[low+]分別是各自子樹中關鍵字最大的結點若
R[low]key不小於這兩個孩子結點的關鍵字則R[low]未違反堆性質以R[low]為根的樹已是堆無須調整;否則必須將R[low]和
它的兩個孩子結點中關鍵字較大者進行交換即R[low]與R[large](R[large]key=max(R[low]keyR[low+]key))交換交
換後又可能使結點R[large]違反堆性質同樣由於該結點的兩棵子樹(若存在)仍然是堆故可重復上述的調整過程對以
R[large]為根的樹進行調整此過程直至當前被調整的結點已滿足堆性質或者該結點已是葉子為止上述過程就象過篩子一樣
把較小的關鍵字逐層篩下去而將較大的關鍵字逐層選上來因此有人將此方法稱為篩選法
具體的算法【參見教材】
②BuildHeap的實現
要將初始文件R[ln]調整為一個大根堆就必須將它所對應的完全二叉樹中以每一結點為根的子樹都調整為堆
顯然只有一個結點的樹是堆而在完全二叉樹中所有序號
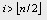
的結點都是葉子
因此以這些結點為根的子樹均已是堆
這樣我們只需依次將以序號為
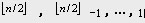
的結點作為根的子樹都調整為堆即可
具體算法【參見教材】
大根堆排序實例
對於關鍵字序列()在建堆過程中完全二叉樹及其存儲結構的變化情況參見
算法分析
堆排序的時間主要由建立初始堆和反復重建堆這兩部分的時間開銷構成它們均是通過調用Heapify實現的
堆排序的最壞時間復雜度為O(nlgn)堆排序的平均性能較接近於最壞性能
由於建初始堆所需的比較次數較多所以堆排序不適宜於記錄數較少的文件
堆排序是就地排序輔助空間為O()
它是不穩定的排序方法
From:http://tw.wingwit.com/Article/program/sjjg/201311/23779.html
