特殊矩陣
所謂特殊矩陣是指非零元素或零元素的分布有一定規律的矩陣
(
在一個n階方陣A中
aij=aji
則稱A為對稱矩陣
【例】下圖便是一個

(
對稱矩陣中的元素關於主對角線對稱
①按
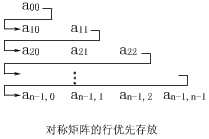
即按a
其中
sa[
sa[
……
sa[n(n+
②元素aij的存放位置
aij元素前有i行(從第
在第i行上
sa[i×(i+
③aij和sa[k]之間的對應關系
若i≥j
若i<j
令I=max(i
k=i×(i+
(
LOC(aij)=LOC(sa[k])
=LOC(sa[
通過下標變換公式
【例】a
k=I×(I+
(
以主對角線劃分
①上三角矩陣
如下圖(a)所示
②下三角矩陣
與上三角矩陣相反
注意
在多數情況下
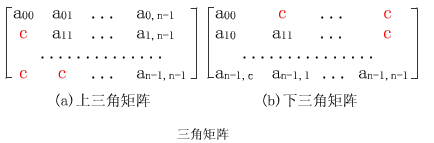
(
三角矩陣中的重復元素c可共享一個存儲空間
① 上三角矩陣中aij和sa[k]之間的對應關系
上三角矩陣中
aij元素前有i行(從第
(n
在第i行上
sa[i×(
所以
┌i×(
k=│
└n×(n+
②下三角矩陣中aij和sa[k]之間的對應關系
┌i×(i+
k=│
└n×(n+
注意
三角矩陣的壓縮存儲結構是隨機存取結構
所有的非零元素集中在以主對角線為中心的帶狀區域中
【例】下圖給出了一個三對角矩陣

其中
非零元素僅出現在主對角上(aii
由此可知
若|i
對角矩陣可按行優先順序或對角線的順序
From:http://tw.wingwit.com/Article/program/sjjg/201311/23770.html
