
(
(
(
答:
(
(a)
(b)無
(c)
(d)無
(
(a)
(b)不是連通圖
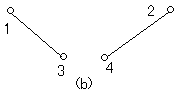
(
(a)不是自由樹
(b)是自由森林
(c)不是自由樹
(d)是自由樹
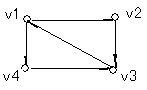
(
(
(
(
答
(
(
有v
v
(
D(v
D(v
D(v
D(v
(
vertex firstedge next
┌─┬─┐ ┌─┬─┐ ┌─┬─┐
├─┼─┤ ├─┼─┤ └─┴─┘
├─┼─┤ ├─┼─┤
├─┼─┤ ├─┼─┤
└─┴─┘ └─┴─┘
逆鄰接表
┌─┬─┐ ┌─┬─┐
├─┼─┤ ├─┼─┤
├─┼─┤ ├─┼─┤ ┌─┬─┐
├─┼─┤ ├─┼─┤ └─┴─┘
└─┴─┘ └─┴─┘
鄰接矩陣
┌ ┓
┌ ┓ |
|
|
|
|
┕ ┙ ┕ ┙
(a) (b)
答:
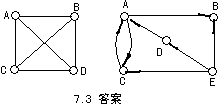
解
鄰接表如下
┌─┬─┐ ┌─┬─┐ ┌─┬─┐
├─┼─┤ ├─┼─┤ ├─┼─┤ ┌─┬─┐
├─┼─┤ ├─┼─┤ ├─┼─┤ ├─┼─┤
├─┼─┤ ├─┼─┤ └─┴─┘ └─┴─┘
├─┼─┤ ├─┼─┤
├─┼─┤ ├─┼─┤
├─┼─┤ ├─┼─┤
└─┴─┘ └─┴─┘
鄰接矩陣如下
(
(
(
答
對於n個頂點的無向圖和有向圖
(
無向圖的邊數=m/
有向圖的邊數=m
(
(
對於有向圖
當用鄰接表表示時
(
對於有向圖
(
對於有向圖
(
對於有向圖
答
n個頂點的連通圖至少有n
答
DFS遍歷采用棧來暫存頂點
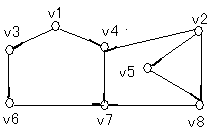
答
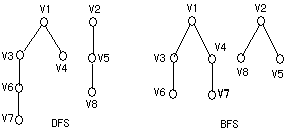
答
相應的鄰接表如下
┌─┬─┐ ┌─┬─┐ ┌─┬─┐ ┌─┬─┐ ┌─┬─┐ ┌─┬─<
From:http://tw.wingwit.com/Article/program/sjjg/201311/23765.html
