利用線性探測法構造散列表
【例
造這組關鍵字的散列表
解答:為了減少沖突 數為:h(key)=key%13。 由除余法的散列函數計算出的上述關鍵字序列的散列地址為(0,10,2,12,5,2,3,12,6,12)。 前5個關鍵字插入時,其相應的地址均為開放地址,故將它們直接插入T[0],T[10),T[2],T[12]和T[5]中。 當插入第6個關鍵字15時,其散列地址2(即h(15)=15%13=2)已被關鍵字41(15和41互為同義詞)占用。故探查h1=(2+1)%13=3, 此地址開放,所以將15放入T[3]中。 當插入第7個關鍵字68時,其散列地址3已被非同義詞15先占用,故將其插入到T[4]中。 當插入第8個關鍵字12時,散列地址12已被同義詞38占用,故探查hl=(12+1)%13=0,而T[0]亦被26占用,再探查h2=(12+2)% 13=1,此地址開放,可將12插入其中。 類似地,第9個關鍵字06直接插入T[6]中;而最後一個關鍵字51插人時,因探查的地址12,0,1,…,6均非空,故51插入 T[7]中。 構造散列表的具體過程【 參見動畫演示 】 聚集或堆積現象 用線性探查法解決沖突時,當表中i,i+1,…,i+k的位置上已有結點時,一個散列地址為i,i+1,…,i+k+1的結點都將插入在 位置i+k+1上。把這種散列地址不同的結點爭奪同一個後繼散列地址的現象稱為聚集或堆積(Clustering)。這將造成不是同義詞的結 點也處在同一個探查序列之中,從而增加了探查序列的長度,即增加了查找時間。若散列函數不好或裝填因子過大,都會使堆積現象 加劇。 【例】上例中,h(15)=2,h(68)=3,即15和68不是同義詞。但由於處理15和同義詞41的沖突時,15搶先占用了T[3],這就使 得插入68時,這兩個本來不應該發生沖突的非同義詞之間也會發生沖突。 為了減少堆積的發生,不能像線性探查法那樣探查一個順序的地址序列(相當於順序查找),而應使探查序列跳躍式地散列在整個 散列表中。 ②二次探查法(Quadratic Probing) 二次探查法的探查序列是: h i =(h(key)+i*i)%m 0≤i≤m-1 //即d i =i 2 即探查序列為d=h(key),d+1 2 ,d+2 2 ,…,等。 該方法的缺陷是不易探查到整個散列空間。 ③雙重散列法(Double Hashing) 該方法是開放定址法中最好的方法之一,它的探查序列是: h i =(h(key)+i*h1(key))%m 0≤i≤m-1 //即d i =i*h1(key) 即探查序列為: d=h(key),(d+h1(key))%m,(d+2h1(key))%m,…,等。 該方法使用了兩個散列函數h(key)和h1(key),故也稱為雙散列函數探查法。 注意: 定義h1(key)的方法較多,但無論采用什麼方法定義,都必須使h1(key)的值和m互素,才能使發生沖突的同義詞地址均勻地分布 在整個表中,否則可能造成同義詞地址的循環計算。 【例】 若m為素數,則h1(key)取1到m-1之間的任何數均與m互素,因此,我們可以簡單地將它定義為: h1(key)=key%(m-2)+1 【例】對例9.1,我們可取h(key)=key%13,而h1(key)=key%11+1。 【例】若m是2的方冪,則h1(key)可取1到m-1之間的任何奇數。 2、拉鏈法 (1)拉鏈法解決沖突的方法 拉鏈法解決沖突的做法是:將所有關鍵字為同義詞的結點鏈接在同一個單鏈表中。若選定的散列表長度為m,則可將散列表定義為 一個由m個頭指針組成的指針數組T[0..m-1]。凡是散列地址為i的結點,均插入到以T[i]為頭指針的單鏈表中。T中各分量的初值均 應為空指針。在拉鏈法中,裝填因子α可以大於1,但一般均取α≤1。 【例9.2】已知一組關鍵字和選定的散列函數和例9.1相同,用拉鏈法解決沖突構造這組關鍵字的散列表。 解答:不妨和例9.1類似,取表長為13,故散列函數為h(key)=key%13,散列表為T[0..12]。 注意: 當把h(key)=i的關鍵字插入第i個單鏈表時,既可插入在鏈表的頭上,也可以插在鏈表的尾上。這是因為必須確定key不在第i個 鏈表時,才能將它插入表中,所以也就知道鏈尾結點的地址。若采用將新關鍵字插入鏈尾的方式,依次把給定的這組關鍵字插入表中 ,則所得到的散列表如下圖所示。 具體構造過程【 參見動畫演示 】。
(2)拉鏈法的優點 與開放定址法相比,拉鏈法有如下幾個優點: (1)拉鏈法處理沖突簡單,且無堆積現象,即非同義詞決不會發生沖突,因此平均查找長度較短; (2)由於拉鏈法中各鏈表上的結點空間是動態申請的,故它更適合於造表前無法確定表長的情況; (3)開放定址法為減少沖突,要求裝填因子α較小,故當結點規模較大時會浪費很多空間。而拉鏈法中可取α≥1,且結點較大 時,拉鏈法中增加的指針域可忽略不計,因此節省空間; (4)在用拉鏈法構造的散列表中,刪除結點的操作易於實現。只要簡單地刪去鏈表上相應的結點即可。而對開放地址法構造的散 列表,刪除結點不能簡單地將被刪結點的空間置為空,否則將截斷在它之後填人散列表的同義詞結點的查找路徑。這是因為各種開放 地址法中,空地址單元(即開放地址)都是查找失敗的條件。因此在用開放地址法處理沖突的散列表上執行刪除操作,只能在被刪結點 上做刪除標記,而不能真正刪除結點。 (3)拉鏈法的缺點 拉鏈法的缺點是:指針需要額外的空間,故當結點規模較小時,開放定址法較為節省空間,而若將節省的指針空間用來擴大散列 表的規模,可使裝填因子變小,這又減少了開放定址法中的沖突,從而提高平均查找速度。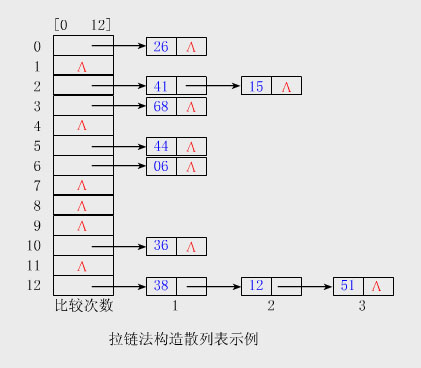
From:http://tw.wingwit.com/Article/program/sjjg/201311/23677.html
