在程序設計中
常用下列三種不同的出錯處理方式
() 用exit語句終止執行並報告錯誤
() 以函數的返回值區別正確返回或錯誤返回
() 設置一個整型變量的函數參數以區別正確返回或某種錯誤返回
試討論這三種方法各自的優缺點
解()exit常用於異常錯誤處理它可以強行中斷程序的執行返回操作系統
()以函數的返回值判斷正確與否常用於子程序的測試便於實現程序的局部控制
()用整型函數進行錯誤處理的優點是可以給出錯誤類型便於迅速確定錯誤
在程序設計中可采用下列三種方法實現輸出和輸入
() 通過scanf和printf語句
() 通過函數的參數顯式傳遞
() 通過全局變量隱式傳遞
試討論這三種方法的優缺點
解()用scanf和printf直接進行輸入輸出的好處是形象直觀但缺點是需要對其進行格式控制較為煩瑣如果出現錯誤則會引起整個系統的崩潰
()通過函數的參數傳遞進行輸入輸出便於實現信息的隱蔽減少出錯的可能
()通過全局變量的隱式傳遞進行輸入輸出最為方便只需修改變量的值即可但過多的全局變量使程序的維護較為困難
設n為正整數試確定下列各程序段中前置以記號@的語句的頻度
() i=; k=;
while(i<=n){
@ k += *i;
i++;
}
() i=; k=;
do {
@ k += *i;
i++;
} while(i<=n);
() i=; k=;
while (i<=n) {
i++;
@ k += *i;
}
() k=;
for(i=; i<=n; i++) {
for(j=i; j<=n; j++)
@ k++;
}
() for(i=; i<=n; i++) {
for(j=; j<=i; j++) {
for(k=; k<=j; k++)
@ x += delta;
}
() i=; j=;
while(i+j<=n) {
@ if(i>j) j++;
else i++;
}
() x=n; y=; // n是不小於的常數
while(x>=(y+)*(y+)) {
@ y++;
}
() x=; y=;
while(y>) {
@ if(x>) { x = ; y; }
else x++;
}

假設n為的乘冪並且n>試求下列算法的時間復雜度及變量count的值(以n的函數形式表示)
int Time(int n) {
count = ;x=;
while(x<n/) {
x *= ;count++;
}
return count;
}
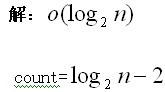
已知有實現同一功能的兩個算法其時間復雜度分別為O(n)和O(n)假設現實計算機可連續運算的時間為秒(多天)又每秒可執行基本操作(根據這些操作來估算算法時間復雜度)次試問在此條件下這兩個算法可解問題的規模(即n值的范圍)各為多少?哪個算法更適宜?請說明理由

則對於同樣的循環次數n在這個規模下第二種算法所花費的代價要大得多故在這個規模下第一種算法更適宜
設有以下三個函數
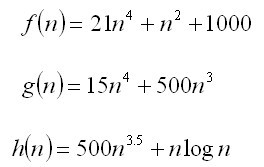
請判斷以下斷言正確與否
() f(n)是O(g(n))
() h(n)是O(f(n))
() g(n)是O(h(n))
() h(n)是O(n)
() h(n)是O(nlogn)
解()對 ()錯 ()錯 ()對 ()錯
試設定若干n值比較兩函數n和 的增長趨勢並確定n在什麼范圍內函數n的值大於
的增長趨勢並確定n在什麼范圍內函數n的值大於 的值
的值

[] [] []
From:http://tw.wingwit.com/Article/program/sjjg/201311/23631.html

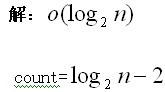

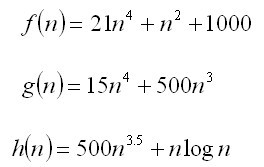
 的增長趨勢
的增長趨勢 的值
的值
