廣義表的概念

　　廣義表(Lists又稱列表)是線性表的推廣即廣義表中放松對表元素的原子限制容許它們具有其自身結構

廣義表定義
　　廣義表是n(n≥)個元素aa…ai…an的有限序列
　其中
　　①ai或者是原子或者是一個廣義表
　　②廣義表通常記作
　　　　　Ls=( aa…ai…an)
　　③Ls是廣義表的名字n為它的長度
　　④若ai是廣義表則稱它為Ls的子表
　注意
　　①廣義表通常用圓括號括起來用逗號分隔其中的元素
　　②為了區分原子和廣義表書寫時用大寫字母表示廣義表用小寫字母表示原子
　　③若廣義表Ls非空(n≥)則al是LS的表頭其余元素組成的表(aa…an)稱為Ls的表尾
　　④廣義表是遞歸定義的

廣義表表示
（）廣義表常用表示
　　① E=()
     　E是一個空表其長度為
　　② L=(ab)
     　L是長度為的廣義表它的兩個元素都是原子因此它是一個線性表
　　③ A=(xL)=(x(ab))
     　A是長度為的廣義表第一個元素是原子x第二個元素是子表L
　　④ B=(Ay)=((x(ab))y)
　     B是長度為的廣義表第一個元素是子表A第二個元素是原子y
　　⑤ C=(AB)=((x(ab))((x(ab))y))
     　C的長度為兩個元素都是子表
　　⑥ D=(aD)=(a(a(a(…))))
     　D的長度為第一個元素是原子第二個元素是D自身展開後它是一個無限的廣義表

（）廣義表的深度
　　一個表的深度是指表展開後所含括號的層數
  【例】表LABC的深度為分別為表D的深度為∞

（）帶名字的廣義表表示
　　如果規定任何表都是有名字的為了既表明每個表的名字又說明它的組成則可以在每個表的前面冠以該表的名字於是上例中的各表又可以寫成
①E()
②L(ab)
③A(xL(ab))
④B(A(xL(ab))y)
⑤C(A(xl(ab))B(A(xL(ab))y))
⑥D(aD(aD(…)))

（）廣義表的圖形表示
（a）廣義表的圖形表示
　　①圖中的分支結點對應廣義表
　　②非分支結點一般是原子
　　③但空表對應的也是非分支結點
　　【例】下圖給出了幾個廣義表的圖形表示

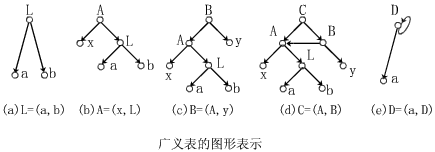
（b）廣義表的圖形形狀劃分
　　①與樹對應的廣義表稱為純表它限制了表中成分的共享和遞歸
　　②允許結點共享的表稱再入表
  【例】上圖(d)子表A是共享結點它既是C的一個元素又是子表B的元素
　　③允許遞歸的表稱為遞歸表
  【例】上圖(e)表D是其自身的子表

（）遞歸表再人表純表線性表之間的關系滿足
      
　　廣義表不僅是線性表的推廣也是樹的推廣

廣義表運算
　　由於廣義表是對線性表和樹的推廣並且具有共享和遞歸特性的廣義表可以和有向圖(見第章)建立對應因此廣義表的大部分運算與這些數據結構上的運算類似
　　在此只討論廣義表的兩個特殊的基本運算取表頭head(Ls)和取表尾tail(Ls)
　　根據表頭表尾的定義可知任何一個非空廣義表的表頭是表中第一個元素它可以是原子也可以是子表而其表尾必定是子表
  【例】
      head(L)=a tail(L)=(b)
      head(B)=A tail(B)=(y)
  由於tail(L)是非空表可繼續分解得到
      head(tail(L))=b tail(tail(L))=()
　對非空表A和(y)也可繼續分解
　注意:
　　廣義表()和(())不同前者是長度為的空表對其不能做求表頭和表尾的運算而後者是長度為l的非空表(只不過該表中惟一的一個元素是空表)對其可進行分解得到的表頭和表尾均是空表()

 

From:http://tw.wingwit.com/Article/program/sjjg/201311/23616.html