樹的概念

本章簡介
 
　　樹形結構是一類重要的非線性結構樹形結構是結點之間有分支並具有層次關系的結構它非常類似於自然界中的樹
　　樹結構在客觀世界中是大量存在的例如家譜行政組織機構都可用樹形象地表示
　　樹在計算機領域中也有著廣泛的應用例如在編譯程序中用樹來表示源程序的語法結構在數據庫系統中可用樹來組織信息在分析算法的行為時可用樹來描述其執行過程
　　本章重點討論二叉樹的存儲表示及其各種運算並研究一般樹和森林與二叉樹的轉換關系最後介紹樹的應用實例

樹的概念

家族樹
　　在現實生活中有入如下血統關系的家族可用樹形圖表示
　　　　張源有三個孩子張明張亮和張麗
　　　　張明有兩個孩子張林和張維
　　　　張亮有三個孩子張平張華和張群
　　　　張平有兩個孩子張晶和張磊  

            
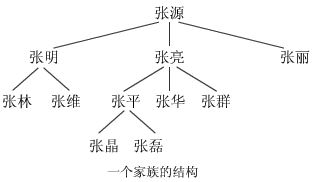
　　以上表示很像一棵倒畫的樹其中樹根是張源樹的分支點是張明張亮和張平該家族的其余成員均是樹葉而樹枝(即圖中的線段)則描述了家族成員之間的關系顯然以張源為根的樹是一個大家庭它可以分成張明張亮和張麗為根的三個小家庭每個小家庭又都是一個樹形結構

樹的定義
　　樹的遞歸定義
　　　樹(Tree)是n(n≥)個結點的有限集TT為空時稱為空樹否則它滿足如下兩個條件
()有且僅有一個特定的稱為根(Root)的結點
()其余的結點可分為m(m≥)個互不相交的子集TlT…Tm其中每個子集本身又是一棵樹並稱其為根的子樹(Subree)
　注意
　　樹的遞歸定義刻畫了樹的固有特性一棵非空樹是由若干棵子樹構成的而子樹又可由若干棵更小的子樹構成

樹的表示
（）樹形圖表示
　　　樹形圖表示是樹結構的主要表示方法
　　樹的樹形圖表示中結點用圓圈表示結點的名字寫在圓圈旁邊（有時亦可寫在圓圈內）

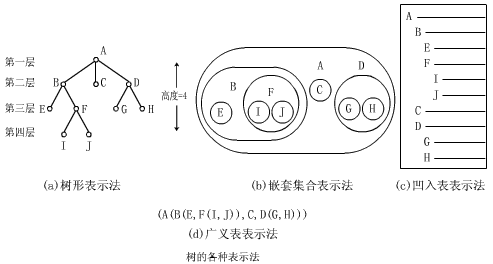
　　　用該定義來分析上圖(a)所示的樹
　圖中的樹由結點的有限集T={ABCDEFCHIJ}所構成其中A是根結點T中其余結點可分成三個互不相交的子集
          T={BEFIJ}
          T={C}
          T={DGH}
　　TT和T是根A的三棵子樹且本身又都是一棵樹例如T其根為B其余結點可分為兩個互不相交的的子集T={E}和T={FIJ}它們都是B的子樹顯然T是只含一個根結點E的樹而T的根F又有兩棵互不相交的子樹{I}和{J}其本身又都是只含一個根結點的樹
　　
（）樹的其他表示法
① 嵌套集合表示法
　　是用集合的包含關系來描述樹結構
　上圖(a)樹的嵌套集合表示法如圖(b)
      
② 凹入表表示法
　　類似於書的目錄上圖(a)樹的凹入表示法如圖(c)

③ 廣義表表示法
　　用廣義表的形式表示的上圖(a)樹的廣義表表示法如圖(d)
　　（A（B（EF（IJ））CD（GH）））

樹結構的基本術語
（）結點的度(Degree)
　　樹中的一個結點擁有的子樹數稱為該結點的度(Degree)
　　一棵樹的度是指該樹中結點的最大度數
　　度為零的結點稱為葉子(Leaf)或終端結點
　　度不為零的結點稱分支結點或非終端結點
　　除根結點之外的分支結點統稱為內部結點
　　根結點又稱為開始結點

（）孩子(Child)和雙親(Parents)
　　樹中某個結點的子樹之根稱為該結點的孩子(Child)或兒子相應地該結點稱為孩子的雙親(Parents)或父親
　　同一個雙親的孩子稱為兄弟(Sibling)

（）祖先(Ancestor)和子孫(Descendant)
①路徑（path）
　　若樹中存在一個結點序列kk…ki使得ki是ki+的雙親(≤i<j)則稱該結點序列是從kl到kj的一條路徑(Path)或道路
　　路徑的長度指路徑所經過的邊(即連接兩個結點的線段)的數目等於j
　注意
　　若一個結點序列是路徑則在樹的樹形圖表示中該結點序列自上而下地通過路徑上的每條邊
　　從樹的根結點到樹中其余結點均存在一條惟一的路徑

②祖先(Ancestor)和子孫(Descendant)
　　若樹中結點k到ks存在一條路徑則稱k是ks的祖先(Ancestor)ks是k的子孫(Descendant)
　　一個結點的祖先是從根結點到該結點路徑上所經過的所有結點而一個結點的子孫則是以該結點為根的子樹中的所有結點
　約定
　　結點k的祖先和子孫不包含結點k本身

（）結點的層數(Level)和樹的高度（Height）
　　結點的層數(Level)從根起算
　　　根的層數為
　　　其余結點的層數等於其雙親結點的層數加
　　雙親在同一層的結點互為堂兄弟
　　樹中結點的最大層數稱為樹的高度(Height)或深度(Depth)
  注意
　　很多文獻中將樹根的層數定義為

（）有序樹(OrderedTree)和無序樹(UnoderedTree)
　　若將樹中每個結點的各子樹看成是從左到右有次序的(即不能互換)則稱該樹為有序樹(OrderedTree)否則稱為無序樹(UnoderedTree)
　注意
　　若不特別指明一般討論的樹都是有序樹

（）森林(Forest)
　　森林(Forest)是m(m≥)棵互不相交的樹的集合
　　樹和森林的概念相近刪去一棵樹的根就得到一個森林反之加上一個結點作樹根森林就變為一棵樹

樹形結構的邏輯特征
　　樹形結構的邏輯特征可用樹中結點之間的父子關系來描述
（） 樹中任一結點都可以有零個或多個直接後繼(即孩子)結點但至多只能有一個直接前趨(即雙親)結點
（） 樹中只有根結點無前趨它是開始結點葉結點無後繼它們是終端結點
（） 祖先與子孫的關系是對父子關系的延拓它定義了樹中結點之間的縱向次序
（） 有序樹中同一組兄弟結點從左到右有長幼之分
　　對這一關系加以延拓規定若k和k是兄弟且k在k的左邊則kl的任一子孫都在k的任一子孫的左邊那麼就定義了樹中結點之間的橫向次序

From:http://tw.wingwit.com/Article/program/sjjg/201311/23584.html