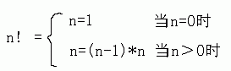調用子程序的含義
在過程和函數的學習中我們知道調用子程序的一般形式是主程序調用子程序A子程序A調用子程序B如圖如示這個過程實際上是
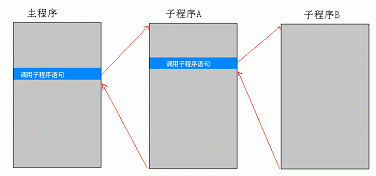
@當主程序執行到調用子程序A語句時系統保存一些必要的現場數據然後執行類似於BASIC語言的GOTO語句跳轉到子程序A(為了說得簡單些我這裡忽略了參數傳遞這個過程)
@當子程序A執行到調用子程序B語句時系統作法如上跳轉到子程序B
@子程序B執行完所有語句後跳轉回子程序A調用子程序B語句的下一條語句(我這又忽略了返回值處理)
@子程序A執行完後跳轉回主程序調用子程序A語句的下一條語句
@主程序執行到結束
做個比較我在吃飯(執行主程序)吃到一半時某人叫我(執行子程序A)話正說到一半電話又響了起來(執行子程序B)我只要先接完電話再和某人把話說完最後把飯吃完(我這飯吃得也夠累的了J)
認識遞歸函數
我們在高中時都學過數學歸納法例
求 n!
我們可以把n!這麼定義
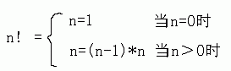
也就是說要求!我們必須先求出!要求!必須先求!要求!就必須先求!而!=所以!=!*=再進而求!!分別用函數表示則如圖

我們可以觀察到除計算!子程序外其他的子程序基本相似我們可以設計這麼一個子程序
int factorial(int i){
int res;
res=factorial(I)*i;
return res;
}
那麼當執行主程序語句s=factorial()時就會執行factorial()但在執行factorial()又會調用factorial()這時大家要注意factorial()和factorial()雖然是同一個代碼段但在內存中它的數據區是兩份!而執行factorial()時又會調用factorial()執行factorial()時又會調用factorial()每調用一次factorial函數它就會在內存中新增一個數據區那麼這些復制了多份的函數大家可以把它看成是多個不同名的函數來理解;
但我們這個函數有點問題在執行factorial()時它又會調用factorial()造成死循環也就是說在factorial函數中我們要在適當的時候保證不再調用該函數也就是不執行res=factorial(I)*i;這條調用語句所以函數要改成
int factorial(int i){
int res;
if (I>) res=factorial(I)*i; else res=;
return res;
}
那麼求!的實際執行過程如圖所示
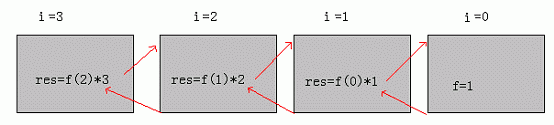
如何考慮用遞歸的方法來解決問題
例求s=++++++……+n
本來這個問題我們過去常用循環累加的方法而這裡如要用遞歸的方法必須考慮兩點
) 能否把問題轉化成遞歸形式的描述;
) 是否有遞歸結束的邊界條件
設:函數s(n)=+++…+(n)+n
顯然遞歸的兩個條件都有了
) s(n) =s(n)+n
) s()=
所以源程序為
int progression(int n){
int res;
if (n= )res= else res=progression(n)+n;
return res;
}
遞歸的應用
中序遍歷二叉樹
void inorder (BinTree T){
if (T){
inorder(T>lchild);
printf(%cT>data);
inorder(T>rchild);
}
}
現假設樹如圖(為了講解方便樹很簡單)
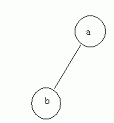
@執行第一次調用inorderT指向頂結點T不為空所以第二次調用inorder;
@T指向頂結點的左子樹結點也就是B不為空所以第三次調用inorder;
@T指向B結點的左子樹結點為空所以什麼都不執行返回inorder;
@打印B結點的DATA域值b;
@第四次調用inorder去訪問B子樹的右結點
@T指向B結點的右子樹結點為空所以什麼都不執行返回inorder;
@返回inorder;
@打印A結點的DATA域值a;
@第五次調用inorder去訪問A子樹的右結點;
@T指向A結點的右子樹結點為空所以什麼都不執行返回inorder;
@inorder執行完畢返回
From:http://tw.wingwit.com/Article/program/sjjg/201311/23539.html