二叉樹的特殊形態
滿二叉樹(Full Binary Tree)一棵深度為k且有k個結點的二叉樹
特點二叉樹的所有分支結點都存在左子樹和右子樹
特點二叉樹的所有葉子結點都在同一層上
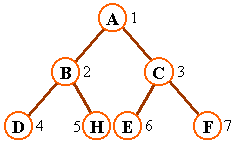
完全二叉樹(Complete Binary Tree)深度為k的有n個結點的二叉樹當且僅當其每一個結點都與深度為k的滿二叉樹中編號從至n的結點一一對應
特點葉子結點只可能在層次最大的兩層上出現
特點對任一結點若其右分支下的子孫的最大層次為L則其左分支下的子孫的最大層次必為 L 或 L+
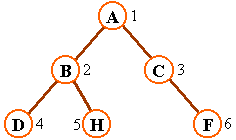
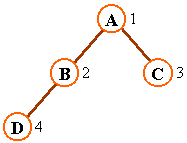
二叉樹的性質
性質 在二叉樹的第i層上至多有i個結點(i≥)
證明歸納法
i=時只有一個根結點顯然i==是對的
現在假定對所有的j≤j<i命題成立即第j層上至多有j個結點那麼可以證明j=i時命題也成立
由歸納假設第i層上至多有i個結點由於二叉樹的每個結點的度至多為故在第i層上的最大結點數為第i層上的最大結點數的倍即×i= i
性質 深度為k的二叉樹至多有k個結點(k≥)
證明
由性質可見深度為k的二叉樹的最大結點數為
性質 對任何一棵二叉樹T如果其終端結點數為n度為的結點數為n則
n=n+
證明:
設n為二叉樹T中度為的結點數
∵ 二叉樹中所有結點的度均小於或等於
∴ n=n+n+n ()
設B為分支總數則n=B+
∵ 這些分支是由度為或的結點射出的
∴ B=n+n
∴ n=n+n+ ()
由式()和()得
n=n+
性質 具有n個結點的完全二叉樹的深度為「logn」+
證明:
假設深度為k則根據性質和完全二叉樹的定義有
k≤n<k
∴ k≤logn<k
∵ k是整數
∴ k=「logn」+
性質 如果對一棵有n個結點的完全二叉樹(其深度為「logn」+)的結點按層
序編號(從第層到第「logn」+層每層從左到右)則對任一結點i
(≤i≤n)有
1如果 i=則結點i是二叉樹的根無雙親如果 i>則其雙親PARENT(i)是結點「i/」
2如果i>n則結點i無左孩子(結點i為葉子結點)否則其左孩子LCHILD(i)是結點i
3如果i+>n則結點i無右孩子否則其右孩子RCHILD(i)是結點i+
From:http://tw.wingwit.com/Article/program/sjjg/201311/23507.html




