二叉樹具有以下重要性質
性質
證明
歸納基礎
歸納假設
歸納步驟
性質
證明
故命題正確
性質
證明
n=no+n
另一方面
nl+
樹中只有根結點不是任何結點的孩子
n=n
由式子
no=n
滿二叉樹和完全二叉樹是二叉樹的兩種特殊情形
一棵深度為k且有
滿二叉樹的特點
(
(
【例】圖(a)是一個深度為
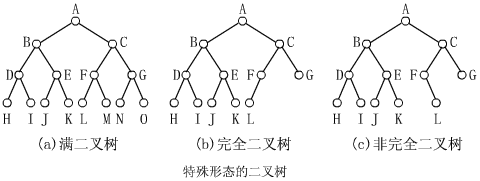
若一棵二叉樹至多只有最下面的兩層上結點的度數可以小於
特點
(
(
(
【例】如圖(c)中
【例】圖(b)是一棵完全二叉樹
性質
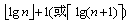
證明
深度為k得完全二叉樹的前k
由於完全二叉樹深度為k
n>
另一方面
n≤
即
由此可推出
k
又因k
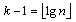
由此即得
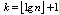
注意
 的證明【參見參考書目】
的證明【參見參考書目】
From:http://tw.wingwit.com/Article/program/sjjg/201311/23284.html
