順序存儲結構
該方法是把二叉樹的所有結點按照一定的線性次序存儲到一片連續的存儲單元中結點在這個序列中的相互位置還能反映出結點之間的邏輯關系
.完全二叉樹結點編號
() 編號辦法
在一棵n個結點的完全二叉樹中從樹根起自上層到下層每層從左至右給所有結點編號能得到一個反映整個二叉樹結構的線性序列
【例】如下圖所示
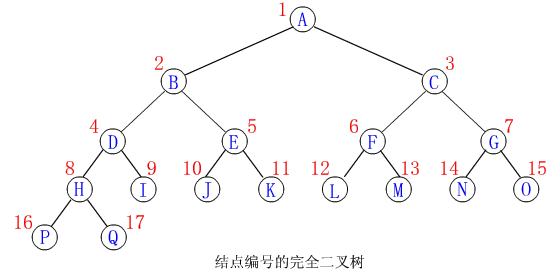
() 編號特點
完全二叉樹中除最下面一層外各層都充滿了結點每一層的結點個數恰好是上一層結點個數的倍從一個結點的編號就可推得其雙親左右孩子兄弟等結點的編號假設編號為i的結點是ki(≤i≤n)則有
①若i>則ki的雙親編號為 若i=則Ki是根結點無雙親
②若i≤n則Ki的左孩子的編號是i否則Ki無左孩子即Ki必定是葉子因此完全二叉樹中編號 的結點必定是葉結點
③若i+≤n則Ki的右孩子的編號是i+否則Ki無右孩子
④若i為奇數且不為則Ki的左兄弟的編號是i否則Ki無左兄弟
⑤若i為偶數且小於n則Ki的右兄弟的編號是i+否則Ki無右兄弟
.完全二叉樹的順序存儲
將完全二叉樹中所有結點按編號順序依次存儲在一個向量bt[n]中
其中
bt[..n]用來存儲結點
bt[]不用或用來存儲結點數目
【例】表是圖所示的完全二叉樹的順序存儲結構bt[]為結點數目b[]的雙親左右孩子分別是bt[]bt[l]和bt[]

.一般二叉樹的順序存儲
() 具體方法
① 將一般二叉樹添上一些 虛結點成為完全二叉樹
② 為了用結點在向量中的相對位置來表示結點之間的邏輯關系按完全二叉樹形式給結點編號
③ 將結點按編號存入向量對應分量其中虛結點用∮表示
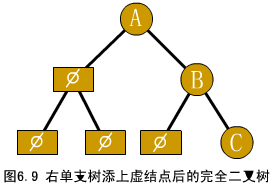
【例】圖中單支樹的順序存儲結構如下圖

() 優點和缺點
① 對完全二叉樹而言順序存儲結構既簡單又節省存儲空間
② 一般的二叉樹采用順序存儲結構時雖然簡單但易造成存儲空間的浪費
【例】最壞的情況下一個深度為k且只有k個結點的右單支樹需要k個結點的存儲空間
③在對順序存儲的二叉樹做插入和刪除結點操作時要大量移動結點
.二叉樹的順序存儲結構類型定義
【參見參考書】
鏈式存儲結構
.結點的結構
二叉樹的每個結點最多有兩個孩子用鏈接方式存儲二叉樹時每個結點除了存儲結點本身的數據外還應設置兩個指針域lchild和rchild分別指向該結點的左孩子和右孩子結點的結構為

.結點的類型說明
typedef char DataType //用戶可根據具體應用定義DataType的實際類型
typedef struct node{
DataType data
Struct node *lchild*rchild //左右孩子指針
}BinTNode //結點類型
typedef BinTNode *BinTree//BinTree為指向BinTNode類型結點的指針類型
.二叉鏈表(二叉樹的常用鏈式存儲結構)
在一棵二叉樹中所有類型為BinTNode的結點再加上一個指向開始結點(即根結點)的BinTree型頭指針(即根指針)root就構成了二叉樹的鏈式存儲結構並將其稱為二叉鏈表
【例】下面左圖所示二叉樹的二叉鏈表如下面中圖所示
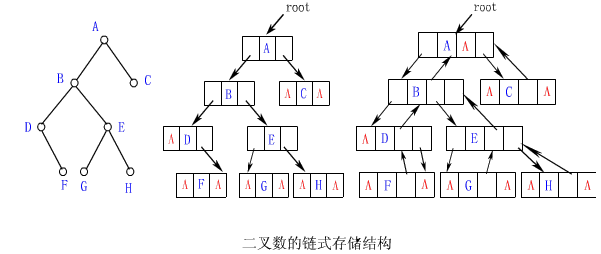
注意
① 一個二叉鏈表由根指針root惟一確定若二叉樹為空則root=NULL若結點的某個孩子不存在則相應的指針為空
② 具有n個結點的二叉鏈表中共有n個指針域其中只有n個用來指示結點的左右孩子其余的n+個指針域為空
.帶雙親指針的二叉鏈表
經常要在二叉樹中尋找某結點的雙親時可在每個結點上再加一個指向其雙親的指針parent形成一個帶雙親指針的二叉鏈表
【例】上面右圖是上面左圖所示的二叉樹的帶雙親指針的二叉鏈表
注意
二叉樹存儲方法的選擇主要依賴於所要實施的各種運算的頻度
From:http://tw.wingwit.com/Article/program/sjjg/201311/23266.html






