最優二叉樹概念
樹的路徑長度是從樹根到樹中每一結點的路徑長度之和
結點的權
結點的帶權路徑長度
樹的帶權路徑長度(Weighted Path Length of Tree)
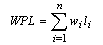
其中
n表示葉子結點的數目
wi和li分別表示葉結點ki的權值和根到結點ki之間的路徑長度
樹的帶權路徑長度亦稱為樹的代價
在權為wl
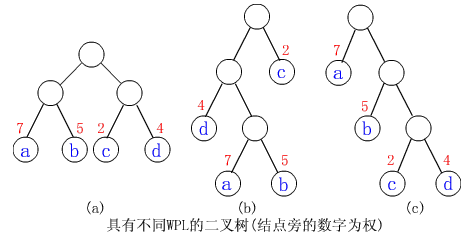
【例】給定
(a)WPL=
(b)WPL=
(c)WPL=
其中(c)樹的WPL最小
注意
① 葉子上的權值均相同時
② 最優二叉樹中
③ 最優二叉樹的形態不唯一
構造最優二叉樹
哈夫曼首先給出了對於給定的葉子數目及其權值構造最優二叉樹的方法
(
(
(
用哈夫曼算法構造哈夫曼樹的過程見【動畫演示】
注意
① 初始森林中的n棵二叉樹
② n個葉子的哈夫曼樹要經過n
③ 哈夫曼樹是嚴格的二叉樹
(
用一個大小為
#define n
#define m
typedef struct { //結點類型
float weight
int lchild
}HTNode
typedef HTNode HuffmanTree[m]
注意
因為C語言數組的下界為
這裡設置parent域有兩個作用
(
在上述存儲結構上實現的哈夫曼算法可大致描述為(設T的類型為HuffmanTree)
(
將T[
(
讀人n個葉子的權值存於向量的前n個分量(即T[
(
對森林中的樹共進行n
①在當前森林T[
② 將根為T[p
將T[p
將T[i]的lchild和rchild分別置為p
新結點T[i]的權值置為T[p
注意
合並後T[pl]和T[p
哈夫曼算法模擬演示過程【參見動畫模擬】
(
void CreateHuffmanTree(HuffmanTree T)
{//構造哈夫曼樹
int i
InitHuffmanTree(T)
InputWeight(T)
for(i=n
SelectMin(T
//在T[
T[p
TIi]
T[j]
T[i]
} // end for
}
上述算法中調用的三個函數【參見練習】
【例】以
From:http://tw.wingwit.com/Article/program/sjjg/201311/23014.html
