二叉樹的遍歷

遍歷概念

　　所謂遍歷(Traversal)是指沿著某條搜索路線依次對樹中每個結點均做一次且僅做一次訪問訪問結點所做的操作依賴於具體的應用問題
　　遍歷是二叉樹上最重要的運算之一是二叉樹上進行其它運算之基礎

遍歷方案

．遍歷方案
　　從二叉樹的遞歸定義可知一棵非空的二叉樹由根結點及左右子樹這三個基本部分組成因此在任一給定結點上可以按某種次序執行三個操作
　　　（）訪問結點本身(N)
　　　（）遍歷該結點的左子樹(L)
　　　（）遍歷該結點的右子樹(R)
以上三種操作有六種執行次序
    　NLRLNRLRNNRLRNLRLN
　注意
　　前三種次序與後三種次序對稱故只討論先左後右的前三種次序

．三種遍歷的命名
　　根據訪問結點操作發生位置命名
　　① NLR前序遍歷(PreorderTraversal亦稱(先序遍歷))
　　　——訪問結點的操作發生在遍歷其左右子樹之前
　　② LNR中序遍歷(InorderTraversal)
　　　——訪問結點的操作發生在遍歷其左右子樹之中(間)
　　③ LRN後序遍歷(PostorderTraversal)
　　　——訪問結點的操作發生在遍歷其左右子樹之後
　注意
　　由於被訪問的結點必是某子樹的根所以N(Node)L(Left subtlee)和R(Right subtree)又可解釋為根根的左子樹和根的右子樹NLRLNR和LRN分別又稱為先根遍歷中根遍歷和後根遍歷

遍歷算法

．中序遍歷的遞歸算法定義
　　若二叉樹非空則依次執行如下操作
　　　　()遍歷左子樹
　　　　()訪問根結點
　　　　()遍歷右子樹

．先序遍歷的遞歸算法定義
　　若二叉樹非空則依次執行如下操作
　　　　() 訪問根結點
　　　　() 遍歷左子樹
　　　　() 遍歷右子樹

．後序遍歷得遞歸算法定義
　　若二叉樹非空則依次執行如下操作
　　　　()遍歷左子樹
　　　　()遍歷右子樹
　　　　()訪問根結點

．中序遍歷的算法實現
　　用二叉鏈表做為存儲結構中序遍歷算法可描述為
      void InOrder(BinTree T)
        { //算法裡①~⑥是為了說明執行過程加入的標號
          ① if(T) { // 如果二叉樹非空
          ②    InOrder(T>lchild)
          ③    printf(％cT>data) // 訪問結點
          ④    InOrder(T>rchild);
          ⑤  }
          ⑥ } // InOrder

遍歷序列

．遍歷二叉樹的執行蹤跡
　　三種遞歸遍歷算法的搜索路線相同（如下圖虛線所示）
具體線路為
　　從根結點出發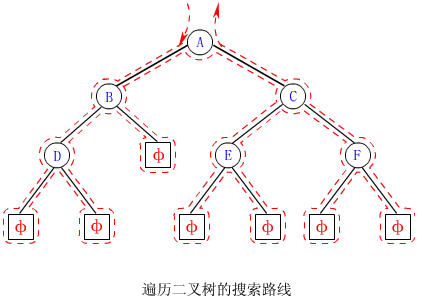逆時針沿著二叉樹外緣移動對每個結點均途徑三次最後回到根結點
      
．遍歷序列
（） 中序序列
　　中序遍歷二叉樹時對結點的訪問次序為中序序列
　　【例】中序遍歷上圖所示的二叉樹時得到的中序序列為
                D B A E C F
（） 先序序列
　　先序遍歷二叉樹時對結點的訪問次序為先序序列
　　【例】先序遍歷上圖所示的二叉樹時得到的先序序列為
                A B D C E F
（） 後序序列
　　後序遍歷二叉樹時對結點的訪問次序為後序序列
　　【例】後序遍歷上圖所示的二叉樹時得到的後序序列為
                D B E F C A
　注意
　　（） 在搜索路線中若訪問結點均是第一次經過結點時進行的則是前序遍歷若訪問結點均是在第二次(或第三次)經過結點時進行的則是中序遍歷(或後序遍歷)只要將搜索路線上所有在第一次第二次和第三次經過的結點分別列表即可分別得到該二叉樹的前序序列中序序列和後序序列
　　（） 上述三種序列都是線性序列有且僅有一個開始結點和一個終端結點其余結點都有且僅有一個前趨結點和一個後繼結點為了區別於樹形結構中前趨(即雙親)結點和後繼(即孩子)結點的概念對上述三種線性序列要在某結點的前趨和後繼之前冠以其遍歷次序名稱
　　【例】上圖所示的二叉樹中結點C其前序前趨結點是D前序後繼結點是E中序前趨結點是E中序後繼結點是F後序前趨結點是F後序後繼結點是A但是就該樹的邏輯結構而言C的前趨結點是A後繼結點是E和F

二叉鏈表的構造

． 基本思想
　　基於先序遍歷的構造即以二叉樹的先序序列為輸入構造
　注意
　　先序序列中必須加入虛結點以示空指針的位置
　【例】
　　建立上圖所示二叉樹其輸入的先序序列是ABD∮∮CE∮∮F∮∮

． 構造算法
　　假設虛結點輸入時以空格字符表示相應的構造算法為
    　void CreateBinTree (BinTree *T)
      { //構造二叉鏈表T是指向根指針的指針故修改*T就修改了實參(根指針)本身
        char ch
        if((ch=getchar())==) *T=NULL //讀人空格將相應指針置空
        else{ //讀人非空格
              *T=(BinTNode *)malloc(sizeof(BinTNode)) //生成結點
              (*T)>data=ch
              CreateBinTree(&(*T)>lchild) //構造左子樹
              CreateBinTree(&(*T)>rchild) //構造右子樹
             }
      }
　注意
　　調用該算法時應將待建立的二叉鏈表的根指針的地址作為實參
　　【例】設root是一根指針(即它的類型是BinTree)則調用CreateBinTree(&root)後root就指向了已構造好的二叉鏈表的根結點
　　　構造二叉鏈表的其他方法【參見參考書目】

二叉樹建立過程見【動畫演示】

二叉樹的應用
　　【參見練習】

 

From:http://tw.wingwit.com/Article/program/sjjg/201311/22857.html