線索二叉樹

線索二叉樹概念

．定義
　　n個結點的二叉鏈表中含有n+個空指針域利用二叉鏈表中的空指針域存放指向結點在某種遍歷次序下的前趨和後繼結點的指針（這種附加的指針稱為線索）
　　這種加上了線索的二叉鏈表稱為線索鏈表相應的二叉樹稱為線索二叉樹(Threaded   BinaryTree)根據線索性質的不同線索二叉樹可分為前序線索二叉樹中序線索二叉樹和後序線索二叉樹三種
　注意
　　線索鏈表解決了二叉鏈表找左右孩子困難的問題出現了無法直接找到該結點在某種遍歷序列中的前趨和後繼結點的問題

．線索鏈表的結點結構
　　線索鏈表中的結點結構為

 
　其中:
　　ltag和rtag是增加的兩個標志域用來區分結點的左右指針域是指向其左右孩子的指針還是指向其前趨或後繼的線索

．線索二叉樹的表示
　【例】下面(a)圖所示的中序線索二叉樹其線索鏈表如下面(b)圖所示

      
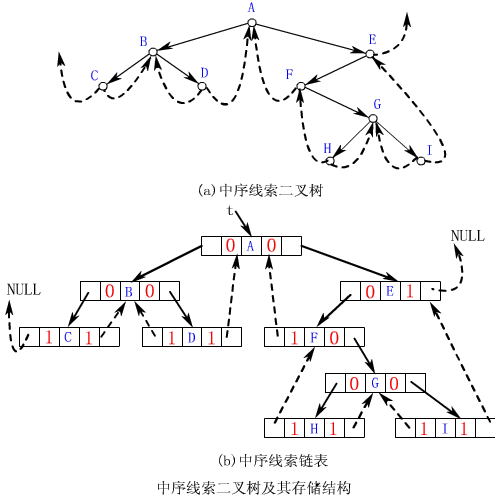
　注意
　　圖中的實線表示指針虛線表示線索
　　結點C的左線索為空表示C是中序序列的開始結點無前趨
　　結點E的右線索為空表示E是中序序列的終端結點無後繼
　　線索二叉樹中一個結點是葉結點的充要條件為左右標志均是

二叉樹的線索化
 
．線索化和線索化實質
　　將二叉樹變為線索二叉樹的過程稱為線索化
　　按某種次序將二叉樹線索化的實質是按該次序遍歷二叉樹在遍歷過程中用線索取代空指針
　　具體過程可【參見動畫演示】

．二叉樹的中序線索化
（）分析
　　算法與中序遍歷算法類似只需要將遍歷算法中訪問結點的操作具體化為建立正在訪問的結點與其非空中序前趨結點間線索
　　該算法應附設一個指針pre始終指向剛剛訪問過的結點（pre的初值應為NULL）而指針p指示當前正在訪問的結點結點*pre是結點*p的前趨而*p是*pre的後繼

（）將二叉樹按中序線索化的算法
  typedef enum { LinkThread} PointerTag //枚舉值Link和Thread分別為
  typedef struct node{
      DataType data
      PointerTag ltagrtag //左右標志
      Struct node *lchild*rchild
    } BinThrNode\\線索二叉樹的結點類型
  typedef BinThrNode *BinThrTree
  BinThrNode *pre=NULL //全局量
  void lnorderThreading(BinThrTree p)
    {//將二叉樹p中序線索化
      if(p){ //p非空時當前訪問結點是*p
             InorderThreading(p>lchild) //左子樹線索化
                 //以下直至右子樹線索化之前相當於遍歷算法中訪問結點的操作
             p>ltag=(p>lchild)?LinkThread //左指針非空時左標志為Link
                                             //(即)否則為Thread(即)
             p>rtag=(p>rchild)?LinkThread
             *(pre){ //若*p的前趨*pre存在
                   if(pre>rtag==Thread) //若*p的前趨右標志為線索
                        pre>rchild=p //令*pre的右線索指向中序後繼
                  if(p>ltag==Thread) //*p的左標志為線索
                       p>lchild=pre //令*p的左線索指向中序前趨
                 } // 完成處理*pre的線索
             pre=p //令pre是下一訪問結點的中序前趨
             InorderThreeding(p>rehild) //右子樹線索化
           }//endif
    } //InorderThreading

（）算法分析
　　和中序遍歷算法一樣遞歸過程中對每結點僅做一次訪問因此對於n個結點的二叉樹算法的時間復雜度亦為O(n)

．二叉樹的前序線索化和後序線索化
　　前序線索化和後序線索化算法與二叉樹的中序線索化類似具體可【參見參考書】

From:http://tw.wingwit.com/Article/program/sjjg/201311/22726.html