選擇合適數據結構解決應用問題
. 計算機處理問題的分類
()數值計算問題
在計算機發展初期人們使用計算機主要是處理數值計算問題
【例.】線性方程的求解
該類問題涉及的運算對象是簡單的整型實型或布爾型數據程序設計者的主要精力集中於程序設計的技巧無須重視數據結構
()非數值性問題
隨著計算機應用領域的擴大和軟硬件的發展非數值性問題越來越顯得重要據統計當今處理非數值性問題占用了%以上的機器時間這類問題涉及到的數據結構更為復雜數據元素之間的相互關系一般無法用數學方程式加以描述因此解決此類問題的關鍵已不再是分析數學和計算方法而是要設計出合適的數據結構才能有效地解決問題
.非數值問題求解
著名的瑞士計算機科學家沃思(NWirth)教授曾提出
算法+數據結構=程序
數據結構是指數據的邏輯結構和存儲結構
算法是對數據運算的描述
程序設計的實質是對實際問題選擇一種好的數據結構加之設計一個好的算法而好的算法在很大程度上取決於描述實際問題的數據結構
【例】電話號碼查詢問題
編一個查詢某個城市或單位的私人電話號碼的程序要求對任意給出的一個姓名若該人有電話號碼則迅速找到其電話號碼否則指出該人沒有電話號碼
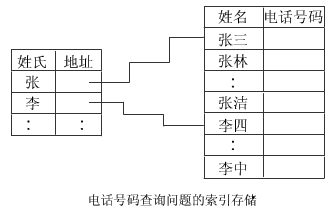
要解此問題首先構造一張電話號碼登記表表中每個結點存放兩個數據項 姓名和電話號碼
要寫出好的查找算法取決於這張表的結構及存儲方式最簡單的方式是將表中結點順序地存儲在計算機中查找時從頭開始依次查對姓名直到找出正確的姓名或是找遍整個表均沒有找到為止這種查找算法對於一個不大的單位或許是可行的但對一個有成千上萬私人電話的城市就不實用了若這張表是按姓氏排列的則可另造一張姓氏索引表采用如下圖所示的存儲結構那麼查找過程是先在索引表中查對姓氏然後根據索引表中的地址到電話號碼登記表中核查姓名這樣查找登記表時就無需查找其它姓氏的名字了因此在這種新的結構上產生的查找算法就更為有效
【例】田徑賽的時間安排問題
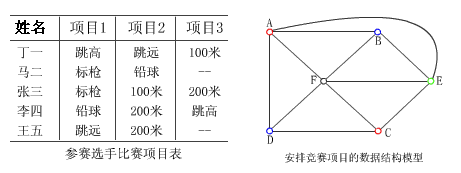
假設某校的田徑選拔賽共設六個項目的比賽即跳高跳遠標槍鉛球米和米短跑規定每個選手至多參加三個項目的比賽現有五名選手報名比賽選手所選擇的項目如參賽選手比賽項目表所示現在要求設計一個競賽日程安排表使得在盡可以短的時間內安排完比賽
()為了能較好地解決這個問題首先應該選擇一個合適的數據結構來表示它表示該問題的數據結構模型圖如右下圖(圖中頂點代表競賽項目在所有的兩個不能同時進行比賽的項目之間連上一條邊)顯然同一個選手選擇的幾個項目是不能在同一時間內比賽的因此該選手選擇的項目中應該兩兩有邊相連
()競賽項目的時間安排問題可以抽象為對無向圖進行著色操作即用盡可能少的顏色去給圖中每個頂點著色使得任意兩個有邊連接的相鄰頂點著上不同的顏色每一種顏色表示一個比賽時間著上同一種顏色的頂點是可以安排在同一時間內競賽的項目由此可得只要安排個不同的時間競賽即可時間內可以比賽跳高(A)和標槍(C)時間內可以比賽跳遠(B)和鉛球(D)時間和時間內分別比賽米(E)和米(F)
解決問題的一個關鍵步驟是選取合適的數據結構表示該問題然後才能寫出有效的算法
From:http://tw.wingwit.com/Article/program/sjjg/201311/22629.html


