求線段交點是一種非常基礎的幾何計算 在很多游戲中都會被使用到
下面我就現學現賣的把最近才學會的一些求線段交點的算法說一說 希望對大家有所幫助
本文講的內容都很初級 主要是面向和我一樣的初學者 所以請各位算法帝們輕拍啊 嘎嘎
引用已知線段(ab) 和線段(cd) 其中a b c d為端點 求線段交點p (平行或共線視作不相交)
算法一 求兩條線段所在直線的交點 再判斷交點是否在兩條線段上
求直線交點時 我們可通過直線的一般方程 ax+by+c= 求得(方程中的abc為系數不是前面提到的端點另外也可用點斜式方程和斜截式方程此處暫且不論)
然後根據交點的與線段端點的位置關系來判斷交點是否在線段上 公式如下圖

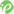
【責編:at
】
算法二 判斷每一條線段的兩個端點是否都在另一條線段的兩側 是則求出兩條線段所在直線的交點 否則不相交
第一步判斷兩個點是否在某條線段的兩側 通常可采用投影法
求出線段的法線向量 然後把點投影到法線上 最後根據投影的位置來判斷點和線段的關系 見下圖

點a和點b在線段cd法線上的投影如圖所示 這時候我們還要做一次線段cd在自己法線上的投影(選擇點c或點d中的一個即可)
主要用來做參考
圖中點a投影和點b投影在點c投影的兩側 說明線段ab的端點在線段cd的兩側
同理 再判斷一次cd是否在線段ab兩側即可
求法線 求投影 什麼的聽起來很復雜的樣子 實際上對於我來說也確實挺復雜在幾個月前我也不會(念書那會兒的幾何知識都忘光了 ( )不過好在學習和實現起來還不算復雜 皆有公式可循
求線段ab的法線
JavaScript Code復制內容到剪貼板var nx=by ayny=ax bxvar normalLine = { x nx y ny }注意 其中 normalLinex和normalLiney的幾何意義表示法線的方向 而不是坐標
求點c在法線上的投影位置
JavaScript Code復制內容到剪貼板var dist= normalLinex*cx + normalLiney*cy
注意 這裡的投影位置是一個標量 表示的是到法線原點的距離 而不是投影點的坐標
通常知道這個距離就足夠了
當我們把圖中 點a投影(distA)點b投影(distB)點c投影(distC) 都求出來之後 就可以很容易的根據各自的大小判斷出相對位置
distA==distB==distC 時 兩條線段共線distA==distB!=distC 時 兩條線段平行distA 和 distB 在distC 同側時 兩條線段不相交
distA 和 distB 在distC 異側時 兩條線段是否相交需要再判斷點c點d與線段ab的關系
前面的那些步驟 只是實現了判斷線段是否相交 當結果為true時 我們還需要進一步求交點
求交點的過程後面再說 先看一下該算法的完整實現
JavaScript Code復制內容到剪貼板function segmentsIntr(a b c d){
//線段ab的法線N var nx = (by ay) ny = (ax bx)
//線段cd的法線N var nx = (dy cy) ny = (cx dx)
//兩條法線做叉乘 如果結果為 說明線段ab和線段cd平行或共線不相交var denominator = nx*ny ny*nxif (denominator==) { return false}
//在法線N上的投影var distC_N=nx * cx + ny * cyvar distA_N=nx * ax + ny * aydistC_Nvar distB_N=nx * bx + ny * bydistC_N
// 點a投影和點b投影在點c投影同側 (對點在線段上的情況本例當作不相交處理)if ( distA_N*distB_N>= ) { return false}
// //判斷點c點d 和線段ab的關系 原理同上// //在法線N上的投影var distA_N=nx * ax + ny * ayvar distC_N=nx * cx + ny * cydistA_Nvar distD_N=nx * dx + ny * dydistA_Nif ( distC_N*distD_N>= ) { return false}
//計算交點坐標var fraction= distA_N / denominatorvar dx= fraction * nydy= fraction * nxreturn { x ax + dx y ay + dy }}
最後 求交點坐標的部分 所用的方法看起來有點奇怪 有種摸不著頭腦的感覺
其實它和算法一 裡面的算法是類似的只是裡面的很多計算項已經被提前計算好了
換句話說 算法二裡求交點坐標的部分 其實也是用的直線的線性方程組來做的
現在來簡單粗略 很不科學的對比一下算法一和算法二 最好情況下 兩種算法的復雜度相同 最壞情況 算法一和算法二的計算量差不多 但是算法二提供了 更多的提前結束條件所以平均情況下應該算法二更優
實際測試下來 實際情況也確實如此
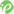
【責編:at
】
算法三 判斷每一條線段的兩個端點是否都在另一條線段的兩側 是則求出兩條線段所在直線的交點 否則不相交
(咦? 怎麼感覺和算法二一樣啊? 不要懷疑 確實一樣 …… 囧)
所謂算法三 其實只是對算法二的一個改良 改良的地方主要就是 不通過法線投影來判斷點和線段的位置關系 而是通過點和線段構成的三角形面積來判斷
先來復習下三角形面積公式 已知三角形三點a(xy) b(xy) c(xy) 三角形面積為
JavaScript Code復制內容到剪貼板var triArea=( (ax cx) * (by cy) (ay cy) * (bx cx) ) /
因為 兩向量叉乘==兩向量構成的平行四邊形(以兩向量為鄰邊)的面積 所以上面的公式也不難理解
而且由於向量是有方向的 所以面積也是有方向的 通常我們以逆時針為正 順時針為負數
改良算法關鍵點就是如果線段ab和點c構成的三角形面積與線段ab和點d構成的三角形面積 構成的三角形面積的正負符號相異那麼點c和點d位於線段ab兩側 如下圖所示

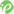
【責編:at
】
From:http://tw.wingwit.com/Article/program/Java/Javascript/201311/25424.html



